题目内容
如图,从一个边长为2的菱形铁皮中剪下一个圆心角为60°的扇形。
(1)求这个扇形的面积(结果保留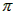 );
);
(2)在剩下的一块余料中,能否从余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由;
(3)当∠B为任意值时,(2)中的结论是否仍然成立?请说明理由。
(1)求这个扇形的面积(结果保留
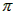 );
);(2)在剩下的一块余料中,能否从余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由;
(3)当∠B为任意值时,(2)中的结论是否仍然成立?请说明理由。
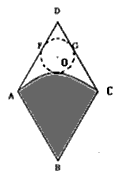
解:(1)如图,
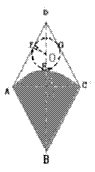
∵AB=AC=2,
∴S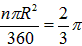 ;
;
(2)连接AC、BD,BD交弧AC于E点,圆心在DE上,
由勾股定理:BD=2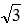 ,DE=2
,DE=2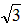 -2≈1.46
-2≈1.46
弧AC的长:l=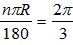 ,
,
∴2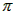 =
=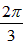 ,
,
∴2r=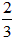 ≈0.67<1.46=DE
≈0.67<1.46=DE
另一方面,如图:由于∠ADE=30°,过O作OF⊥AD,则OD=2OF=2r,因此DE≥3r,
所以能在余料中剪出一个圆作为底面与此扇形围成圆锥;
(3)当∠B=90°时,不能剪出一个圆作为底面与此扇形围成圆锥,理由如下:
弧AC的长:l=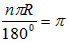 ,2
,2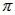 r=
r=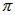 ,
,
∴2r=1
由勾股定理求得:BD=2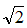 ,DE=2
,DE=2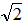 -2≈0.82<1=2r,
-2≈0.82<1=2r,
因此∠B为任意值时,(2)中的结论不一定成立。

∵AB=AC=2,
∴S
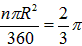 ;
;(2)连接AC、BD,BD交弧AC于E点,圆心在DE上,
由勾股定理:BD=2
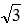 ,DE=2
,DE=2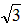 -2≈1.46
-2≈1.46弧AC的长:l=
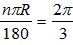 ,
, ∴2
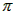 =
=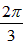 ,
,∴2r=
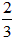 ≈0.67<1.46=DE
≈0.67<1.46=DE 另一方面,如图:由于∠ADE=30°,过O作OF⊥AD,则OD=2OF=2r,因此DE≥3r,
所以能在余料中剪出一个圆作为底面与此扇形围成圆锥;
(3)当∠B=90°时,不能剪出一个圆作为底面与此扇形围成圆锥,理由如下:
弧AC的长:l=
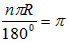 ,2
,2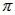 r=
r=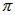 ,
,∴2r=1
由勾股定理求得:BD=2
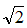 ,DE=2
,DE=2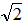 -2≈0.82<1=2r,
-2≈0.82<1=2r,因此∠B为任意值时,(2)中的结论不一定成立。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
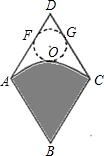 如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.
如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.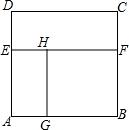 如图,从一个边长为a的正方形纸片ABCD中剪去一个宽为b的长方形CDEF,再从剩下的纸片中沿平行短边的方向剪去一个边长为c的正方形BFHG,若长方形CDEF与AGHE的面积比是3:2,那么
如图,从一个边长为a的正方形纸片ABCD中剪去一个宽为b的长方形CDEF,再从剩下的纸片中沿平行短边的方向剪去一个边长为c的正方形BFHG,若长方形CDEF与AGHE的面积比是3:2,那么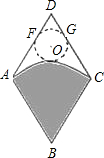 如图,从一个边长为2的菱形铁皮中剪下一个圆心角为60°的扇形.
如图,从一个边长为2的菱形铁皮中剪下一个圆心角为60°的扇形. 如图,从一个边长为1米的正方形铁皮中剪下一个扇形.
如图,从一个边长为1米的正方形铁皮中剪下一个扇形. );
);