题目内容
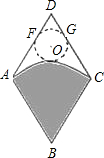 如图,从一个边长为2的菱形铁皮中剪下一个圆心角为60°的扇形.
如图,从一个边长为2的菱形铁皮中剪下一个圆心角为60°的扇形.(1)求这个扇形的面积(结果保留π).
(2)在剩下的一块余料中,能否从余料中剪出一个圆作为底面与此扇形围成一个圆锥请说明理由.
(3)当∠B为任意值时,(2)中的结论是否仍然成立?请说明理由.
分析:(1)扇形的面积公式是:S=
,代入公式就可以求出扇形的面积;
(2)、(3)要判断能否从余料剪出一个圆与此扇形围成一个圆锥,就是比较余料部分的内切圆的半径与圆锥的底面半径的大小关系.
| nπr2 |
| 360 |
(2)、(3)要判断能否从余料剪出一个圆与此扇形围成一个圆锥,就是比较余料部分的内切圆的半径与圆锥的底面半径的大小关系.
解答: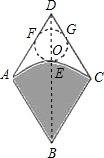 解:(1)如图,
解:(1)如图,
∵BA=BC=2,
∴S=
=
π;
(2)连接AC、BD,BD交弧AC于E点,圆心在DE上,
由勾股定理:BD=2
;
DE=2
-2≈1.46,
弧AC的长:l=
=
;
∴2πr=
,
∴2r=
≈0.67<1.46=DE;
另一方面,如图:由于∠ADE=30°,过O作OF⊥AD,则OD=2OF=2r,因此DE≥3r;
所以能在余料中剪出一个圆作为底面与此扇形围成圆锥.
(3)当∠B=90°时,不能剪出一个圆作为底面与此扇形围成圆锥.
理由:假设能成立,则弧AC的长:l=
=π,
则设圆锥的底面半径是r,则2πr=π,
则r=
.
∴底面直径长是:2r=1;
由勾股定理求得:
BD=2
,DE=2
-2≈0.82<1=2r;
因此∠B为任意值时,(2)中的结论不一定成立.
 解:(1)如图,
解:(1)如图,∵BA=BC=2,
∴S=
| nπR2 |
| 360 |
| 2 |
| 3 |
(2)连接AC、BD,BD交弧AC于E点,圆心在DE上,
由勾股定理:BD=2
| 3 |
DE=2
| 3 |
弧AC的长:l=
| nπR |
| 180 |
| 2π |
| 3 |
∴2πr=
| 2π |
| 3 |
∴2r=
| 2 |
| 3 |
另一方面,如图:由于∠ADE=30°,过O作OF⊥AD,则OD=2OF=2r,因此DE≥3r;
所以能在余料中剪出一个圆作为底面与此扇形围成圆锥.
(3)当∠B=90°时,不能剪出一个圆作为底面与此扇形围成圆锥.
理由:假设能成立,则弧AC的长:l=
| 90π×2 |
| 180 |
则设圆锥的底面半径是r,则2πr=π,
则r=
| 1 |
| 2 |
∴底面直径长是:2r=1;
由勾股定理求得:
BD=2
| 2 |
| 2 |
因此∠B为任意值时,(2)中的结论不一定成立.
点评:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
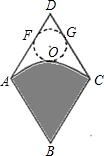 如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.
如图,从一个边长为2米的菱形铁皮中剪下一个圆形角为60°的扇形.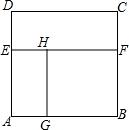 如图,从一个边长为a的正方形纸片ABCD中剪去一个宽为b的长方形CDEF,再从剩下的纸片中沿平行短边的方向剪去一个边长为c的正方形BFHG,若长方形CDEF与AGHE的面积比是3:2,那么
如图,从一个边长为a的正方形纸片ABCD中剪去一个宽为b的长方形CDEF,再从剩下的纸片中沿平行短边的方向剪去一个边长为c的正方形BFHG,若长方形CDEF与AGHE的面积比是3:2,那么 如图,从一个边长为1米的正方形铁皮中剪下一个扇形.
如图,从一个边长为1米的正方形铁皮中剪下一个扇形. );
);