题目内容
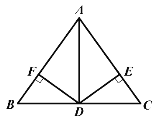
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
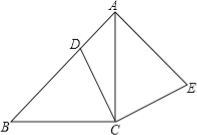
(1)求证:AB⊥AE;
(2)若BC2=ADAB,求证:四边形ADCE为正方形.
【答案】(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论。
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形。
【解析】
(1)根据旋转的性质得到∠DCE=90°,CD=CE,利用等角的余角相等得∠BCD=∠ACE,然后根据“SAS”可判断△BCD≌△ACE,则∠B=∠CAE=45°,所以∠DAE=90°,即可得到结论。
(2)由于BC=AC,则AC2=ADAB,根据相似三角形的判定方法得到△DAC∽△CAB,则∠CDA=∠BCA=90°,可判断四边形ADCE为矩形,利用CD=CE可判断四边形ADCE为正方形。
证明:(1)∵∠ACB=90°,AC=BC,∴∠B=∠BAC=45°。
∵线段CD绕点C顺时针旋转90°至CE位置,∴∠DCE=90°,CD=CE。
∵∠ACB=90°,∴∠ACB﹣∠ACD=∠DCE﹣∠ACD,即∠BCD=∠ACE。
∵在△BCD和△ACE中,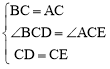 ,
,
∴△BCD≌△ACE(SAS)。∴∠B=∠CAE=45°。
∴∠BAE=45°+45°=90°。∴AB⊥AE。
(2)∵BC2=ADAB,BC=AC,∴AC2=ADAB。∴![]() 。
。
∵∠DAC=∠CAB,∴△DAC∽△CAB。∴∠CDA=∠BCA=90°。
∵∠DAE=90°,∠DCE=90°,∴四边形ADCE为矩形。
∵CD=CE,∴四边形ADCE为正方形。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案