题目内容
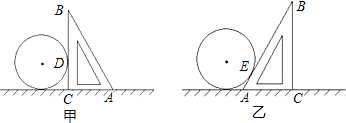
课题学习小组的同学接受了测量一种圆柱形工件直径的任务，他们使用的工具是一个锐角为60°的直角三角板和一把刻度尺．小明的测量方法如图甲，测得DC=9cm，点D为切点．小亮的测量方法如图乙，点E为切点．假设他们的测量结果都是正确的．则与EA的长最接近的整数是（ ）
| A、8cm | B、7cm | C、6cm | D、5cm |
分析：先计算出EA的长，由于图甲测得CD=9即圆的半径等于9，在图乙中直角三角形OAE中利用30度角的三角函数可求得tan30°=
=
，解得AE的值为3
．先估计
的近似值，再求解．
| ||
| 3 |
| AE |
| 9 |
| 3 |
| 3 |
解答：解：∵DC=9cm，
∴tan30°=
=
，
解得AE=3
．
∵1＜
＜2
∴3＜3
＜6．
故选D．
∴tan30°=
| ||
| 3 |
| AE |
| 9 |
解得AE=3
| 3 |
∵1＜
| 3 |
∴3＜3
| 3 |
故选D．
点评：本题考查的是切线的性质，解直角三角形和无理数的估算．估算无理数的近似值在实际生活中有着广泛的应用，我们应熟练掌握．
练习册系列答案
相关题目
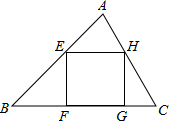某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨：
不妨设
，三条边上的对应高分别为
，内接正方形的边长分别为
.若你对本小题证明有困难，可直接用“
”这个结论，但在证明正确的情况下扣1分）.
形的内接正方形的有关问题进行了探讨：
同学的结果正确吗？若不正确，请举出一个反例并通过计算给予说明，若正确，请给出证明；
C的三条边分别为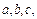
不妨设
，三条边上的对应高分别为
，内接正方形的边长分别为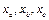
.若你对本小题证明有困难，可直接用
“
”这个结论，但在证明正确的情况下扣1分）.
不妨设
，三条边上的对应高分别为
，内接正方形的边长分别为
.若你对本小题证明有困难，可直接用“
”这个结论，但在证明正确的情况下扣1分）.