Question

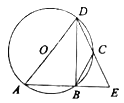
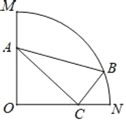
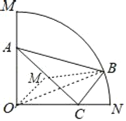
【题目】如图，在扇形OMN中，∠MON＝90°，OM＝6，△ABC是扇形的内接三角形，其中A、C、B分别在半径OM、ON和弧MN上，∠ACB＝90°，BC：AC＝3：8，则线段BC的最小值为_____．

Answer 1

【答案】2

【解析】

如图，取AC的中点M，连接BM，OM，BO，根据BC：AC＝3：8设BC＝3k，AC＝8k，则CM＝AM＝4k，利用勾股定理进一步求解得出BM的长，然后利用BM+OM≥OB进一步求解即可.

如图，取AC的中点M，连接BM，OM，BO，

∵BC：AC＝3：8，

∴可以假设BC＝3k，AC＝8k，则CM＝AM＝4k，

∵∠ACB＝∠COA＝90°，

∴BM＝＝5k，OM＝AC＝4k，

∵BM+OM≥OB，

∴5k+4k≥6，

∴k≥，

∴k的最小值为，

∴BC的最小值为3×＝2，

故答案为2．