题目内容
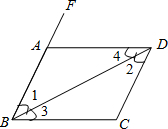 填空(如图所示)
填空(如图所示)(1)因为AD∥BC,所以∠FAD=
∠ABC
∠ABC
(2)因为∠1=∠2,所以
DC
DC
∥AB
AB
(3)因为AD∥BC,所以
∠3=∠4
∠3=∠4
.分析:(1)根据平行线的性质知,同位角∠FAD=∠ABC;
(2)根据平行线的判定定理:内错角相等,两直线平行进行填空;
(3)由平行线的性质知,内错角相等.
(2)根据平行线的判定定理:内错角相等,两直线平行进行填空;
(3)由平行线的性质知,内错角相等.
解答:解:(1)∵AD∥BC,
∴∠FAD=∠ABC(两直线平行,同位角相等).
故答案是:∠ABC;
(2)∵∠1=∠2,
∴DC∥AB(内错角相等,两直线平行);
故答案是:DC、AB;
(3)∵AD∥BC,
∴∠3=∠4(两直线平行,内错角相等).
故答案是:∠3=∠4.
∴∠FAD=∠ABC(两直线平行,同位角相等).
故答案是:∠ABC;
(2)∵∠1=∠2,
∴DC∥AB(内错角相等,两直线平行);
故答案是:DC、AB;
(3)∵AD∥BC,
∴∠3=∠4(两直线平行,内错角相等).
故答案是:∠3=∠4.
点评:本题考查了平行线的判定.平行线的判定与性质的联系与区别:
区别:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.
联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关.
区别:性质由形到数,用于推导角的关系并计算;判定由数到形,用于判定两直线平行.
联系:性质与判定的已知和结论正好相反,都是角的关系与平行线相关.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
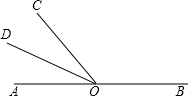 解:∵O是直线AB上一点
解:∵O是直线AB上一点 24、完成推理填空:如图所示,已知AD=BC,AB=DC,试判断∠A与∠ABC的关系.下面是小颖同学的推导过程:
24、完成推理填空:如图所示,已知AD=BC,AB=DC,试判断∠A与∠ABC的关系.下面是小颖同学的推导过程: 推理填空.如图所示.因为∠1=∠DEF(已知).所以
推理填空.如图所示.因为∠1=∠DEF(已知).所以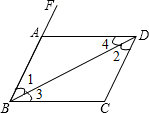 填空(如图所示)
填空(如图所示)