Question

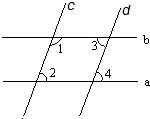9、如图，要得到a∥b，则需要条件（　　）

A、∠2=∠4

B、∠1+∠3=180°

C、∠1+∠2=180°

D、∠2=∠3

Answer 1

分析：在复杂的图形中具有相等关系的两角要判断它们是否是同位角、内错角或同旁内角，被判断平行的两直线是否由“三线八角”而产生的被截直线．

解答：解：A、∵∠2=∠4，
∴c∥d（同位角相等，两直线平行）；
B、∵∠1+∠3=180°，
c∥d（同旁内角互补，两直线平行）；
C、∵∠1+∠2=180°，
∴a∥b（同旁内角互补，两直线平行）；
D、∠2与∠3不能构成三线八角，无法判定两直线平行．
故选C．

点评：正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．