题目内容
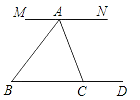
 28、如图,要得到MN∥BC的结论,则需要角相等的条件是
28、如图,要得到MN∥BC的结论,则需要角相等的条件是∠MAB=∠B,∠NAC=∠ACB,∠MAC=∠ACD
(写出两个正确的条件即可).分析:要判定MN∥BC,在图中发现MN、BC分别被直线AB、AC所截,可围绕截线找同位角、内错角和同旁内角.
解答:解:如果∠MAB=∠B,那么MN∥BC(内错角相等,两直线平行);
如果∠NAC=∠ACB,那么MN∥BC(内错角相等,两直线平行);
如果∠MAC=∠ACD,那么MN∥BC(内错角相等,两直线平行).
答:∠MAB=∠B,∠NAC=∠ACB,∠MAC=∠ACD.
如果∠NAC=∠ACB,那么MN∥BC(内错角相等,两直线平行);
如果∠MAC=∠ACD,那么MN∥BC(内错角相等,两直线平行).
答:∠MAB=∠B,∠NAC=∠ACB,∠MAC=∠ACD.
点评:本题答案不唯一,解答此类要判定两直线平行的题,可围绕截线找同位角、内错角和同旁内角.本题是一道探索性条件开放性题目,能有效地培养“执果索因”的思维方式与能力.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目

 ,cos41°=
,cos41°=

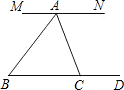 如图,要得到MN∥BC的结论,则需要角相等的条件是________(写出两个正确的条件即可).
如图,要得到MN∥BC的结论,则需要角相等的条件是________(写出两个正确的条件即可).