题目内容
如图,网格中的每个四边形都是菱形.如果格点三角形ABC的面积为S,按照如图所示方式得到格点三角形A1B1C1,格点三角形A2B2C2,格点三角形A3B3C3,则格点三角形A3B3C3的面积为( )
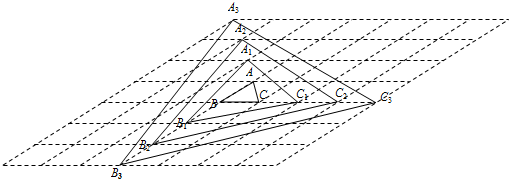

分析:设网络中每个小菱形的边长为一个单位,由于ABC的面积为S,则小菱形的面积为2S;从图上观察可知三角形A2B2C2三个顶点分别在边长为3个单位的菱形的内部,其中一顶点与菱形重合,另两顶点在与前一顶点不相连的两边上,三角形AnBnCn三顶点分别在边长为2n+1个单位的菱形的内部,此菱形与三角形AnBnCn不重合的部分为三个小三角形;由此得到关于三角形AnBnCn面积公式,把n=3代入即可求出三角形A3B3C3的面积.
解答:解:设网络中每个小菱形的边长为一个单位,由于ABC的面积为S,则小菱形的面积为2S;从图上观察可知三角形A2B2C2三个顶点分别在边长为3个单位的菱形的内部,其中一顶点与菱形重合,另两顶点在与前一顶点不相连的两边上,三角形AnBnCn三顶点分别在边长为2n+1个单位的菱形的内部,此菱形与三角形AnBnCn不重合的部分为三个小三角形;而三角形AnBnCn面积=边长为2n+1个单位的菱形面积-三个小三角形面积
=2S(2n+1)2-
-
-
,
=S(8n2+8n+2-2n2-n-2n2-3n-1-n2-n),
=S(3n2+3n+1),
把n=3分别代入上式得:S3=S(3×32+3×3+1)=37S.
故选C.
=2S(2n+1)2-
| (2n+1)×n×2S |
| 2 |
| (2n+1)×(n+1)×2S |
| 2 |
| n×(n+1)×2S |
| 2 |
=S(8n2+8n+2-2n2-n-2n2-3n-1-n2-n),
=S(3n2+3n+1),
把n=3分别代入上式得:S3=S(3×32+3×3+1)=37S.
故选C.
点评:此题主要考查菱形的性质,也考查了学生的读图能力以及探究问题的规律并有规律解决问题的能力.

练习册系列答案
相关题目
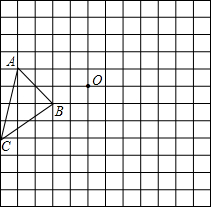

 16、正方形网格中,每个小格的顶点叫做格点.当所作正方形边上的点刚好在格点上的点称为整点.如图中A1B1C1D1四条边上的整点共有8个;A2B2C2D2四条边上的整点共有16个.请你观察图中正方形A3B3C3D3四条边上的整点的个数…按此规律,推算出正方形A10B10C10D10四条边上的整点共有
16、正方形网格中,每个小格的顶点叫做格点.当所作正方形边上的点刚好在格点上的点称为整点.如图中A1B1C1D1四条边上的整点共有8个;A2B2C2D2四条边上的整点共有16个.请你观察图中正方形A3B3C3D3四条边上的整点的个数…按此规律,推算出正方形A10B10C10D10四条边上的整点共有
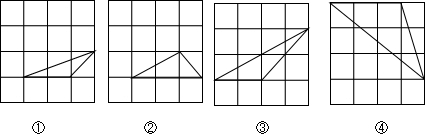
 如图所示的正方形网格中,每个小正方形的边长为1,以方格的格点作一个四边形,则四边形的四条边及两条对角线共六条线段中,其长度是无理数的有( )条.
如图所示的正方形网格中,每个小正方形的边长为1,以方格的格点作一个四边形,则四边形的四条边及两条对角线共六条线段中,其长度是无理数的有( )条.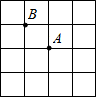 已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示.若点C、D也在小方格的顶点上,这四点正好是一个平行四边形的四个顶点,且这个平行四边形的面积恰好为2,则这样的平行四边形有
已知在正方形网格中,每个小方格都是边长为1的正方形,A、B两点在小方格的顶点上,位置如图所示.若点C、D也在小方格的顶点上,这四点正好是一个平行四边形的四个顶点,且这个平行四边形的面积恰好为2,则这样的平行四边形有