题目内容
【题目】如图，已知AB＝AC，CD⊥AB于D，BE⊥AC于E，BE与CD相交于点O．
（1）问题探究：线段OB，OC有何数量关系，并说明理由；
（2）问题拓展：分别连接OA，BC，试判断直线OA，BC的位置关系，并说明理由；
（3）问题延伸：将题目条件中的“CD⊥AB于D，BE⊥AC于E”换成“D、E分别为AB，AC边上的中点”，（1）（2）中的结论还成立吗？请直接写出结论，不必说明理由．
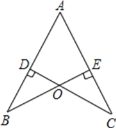
【答案】（1）OB=OC，理由见解析；（2） AO⊥BC，理由见解析；（3） （1）（2）中的结论还成立，理由见解析．
【解析】
（1）根据垂直定义求出∠ADC=∠AEB=90°，根据AAS推出△ADC≌△AEB，根据全等得出AD=AE，∠B=∠C，得出BD=CE，根据AAS推出△BDO≌△CEO即可得出结论；
（2）延长AO交BC于M，根据SAS推出△OBA≌△OCA，根据全等得出∠BAO=∠CAO，根据等腰三角形的性质推出即可；
（3）求出AD=AE，BD=CE，根据SAS推出△ADC≌△AEB，根据全等三角形的性质得出∠DBO=∠ECO，根据AAS推出△BDO≌△CEO，根据全等三角形的性质得出OB=OC，根据SAS推出△OBA≌△OCA，推出∠BAO=∠CAO，根据等腰三角形的性质得出即可．
（1）∵CD⊥AB，BE⊥AC，∴∠ADC=∠AEB=90°，
在△ADC和△AEB中，
∵
，
∴△ADC≌△AEB（AAS），∴AD=AE，∠B=∠C．
∵AB=AC，∴BD=CE，
在△BDO和△CEO中，
∵
，
∴△BDO≌△CEO（AAS），∴OB=OC；
（2）AO⊥BC．理由如下：
延长AO交BC于M．
在△OBA和△OCA中，
∵
，
∴△OBA≌△OCA（SAS），
∴∠BAO=∠CAO．
∵AB=AC，∴AO⊥BC；
（3）（1）（2）中的结论还成立．理由如下：
∵D、E分别为AB，AC边上的中点，AC=AB，∴AD=AE，BD=CE，
在△ADC和△AEB中，
∵
，∴△ADC≌△AEB（SAS），∴∠DBO=∠ECO，
在△BDO和△CEO中，
∵
，∴△BDO≌△CEO（AAS），∴OB=OC，
在△OBA和△OCA中，
∵，∴△OBA≌△OCA（SAS），∴∠BAO=∠CAO．
∵AB=AC，∴AO⊥BC．
