题目内容
已知:在四边形ABCD中,AB=1,E、F、G、H分别时AB、BC、CD、DA上的点,且AE=BF=CG=DH.设四边形EFGH的面积为S,AE=x(0≤x≤1).(1)如图①,当四边形ABCD为正方形时,
①求S关于x的函数解析式,并求S的最小值S0;
②在图②中画出①中函数的草图,并估计S=0.6时x的近似值(精确到0.01);
(2)如图③,当四边形ABCD为菱形,且∠A=30°时,四边形EFGH的面积是否存在最小值?若存在,求出最小值;若不存在,请说明理由.

分析:(1)①四边形ABCD为正方形,易得四边形EFGH为正方形,那么面积S=HE2,可求得二次函数的最值;②看二次函数上y=0.6时对应的x的值即可.
(2)易得△AEH≌△CGF,△EBF≌△GDH.那么四边形EFGH的面积=菱形ABCD的面积-2(S△AHE+S△EBF)利用30°的三角函数值求得两三角形边上的高即可求解.
(2)易得△AEH≌△CGF,△EBF≌△GDH.那么四边形EFGH的面积=菱形ABCD的面积-2(S△AHE+S△EBF)利用30°的三角函数值求得两三角形边上的高即可求解.
解答: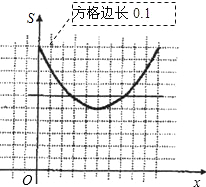 解:(1)①在Rt△AEH中,AE=x,AH=1-x,
解:(1)①在Rt△AEH中,AE=x,AH=1-x,
则S=HE2=x2+(1-x)2
=2x2-2x+1=2(x-
)2+
∴当x=
时,S0=
②列表:
在直角坐标系中描点、画图(图2中粗线).
(注:作图时,不列对应值表不扣分)
观察函数的图象,可知当S=0.6时,x≈0.27和x≈0.73.
验证:当x=0.27时,S=0.6029;当x=0.28时,S=0.5984.
从而取x≈0.28.同理取x≈0.72.
(2)四边形EFGH的面积存在最小值.
理由如下: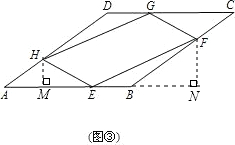
由条件,易证△AEH≌△CGF,△EBF≌△GDH
作HM⊥AE于M,作FN⊥EB且FN交EB的延长线于N
∵AE=x,则AH=1-x
又在Rt△AMH中,∠HAM=30°
∴HM=
AH=
(1-x)
同理得FN=
BF=
x
∴S△AEH=
AE•HM=
x(1-x),S△EBF=
EB•FN=
x(1-x)
又∵SABCD=
∴S=
-4×
x(1-x)=x2-x+
=(x-
)2+
∴当x=
时,四边形EFGH的面积存在最小值
.
 解:(1)①在Rt△AEH中,AE=x,AH=1-x,
解:(1)①在Rt△AEH中,AE=x,AH=1-x,则S=HE2=x2+(1-x)2
=2x2-2x+1=2(x-
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 1 |
| 2 |
②列表:
| x | 0 | 0.3 | 0.5 | 0.7 | 1 |
| S | 0.58 | 0.5 | 0.58 | 0 |
(注:作图时,不列对应值表不扣分)
观察函数的图象,可知当S=0.6时,x≈0.27和x≈0.73.
验证:当x=0.27时,S=0.6029;当x=0.28时,S=0.5984.
从而取x≈0.28.同理取x≈0.72.
(2)四边形EFGH的面积存在最小值.
理由如下:

由条件,易证△AEH≌△CGF,△EBF≌△GDH
作HM⊥AE于M,作FN⊥EB且FN交EB的延长线于N
∵AE=x,则AH=1-x
又在Rt△AMH中,∠HAM=30°
∴HM=
| 1 |
| 2 |
| 1 |
| 2 |
同理得FN=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△AEH=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
又∵SABCD=
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴当x=
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查特殊四边形与二次函数的综合应用.注意二次函数中一个y值有可能对应两个x值.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目

 已知:在Rt△ABC中,∠ABC=90°,以直角边AB为直径作⊙O,⊙O与斜边AC交于点D,E为BC边的中点,连接DE.
已知:在Rt△ABC中,∠ABC=90°,以直角边AB为直径作⊙O,⊙O与斜边AC交于点D,E为BC边的中点,连接DE.
 如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.
如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.