题目内容
 如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.
如图,已知,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,CD=4cm,∠ABC=∠DCB,求BC的长.分析:根据两直线平行,同旁内角互补求出∠ABC=60°,再求出∠DBC=30°,然后利用三角形内角和定理求出∠BDC=90°,然后根据直角三角形30°角所对的直角边等于斜边的一半可得BC=2CD.
解答:解:∵AD∥BC,∠A=120°,
∴∠ABC=180°-120°=60°,
∵BD平分∠ABC,
∴∠DBC=
∠ABC=
×60°=30°,
又∵∠ABC=∠DCB=60°,
∴∠BDC=180°-30°-60°=90°,
∴BC=2CD=2×4=8cm.
∴∠ABC=180°-120°=60°,
∵BD平分∠ABC,
∴∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ABC=∠DCB=60°,
∴∠BDC=180°-30°-60°=90°,
∴BC=2CD=2×4=8cm.
点评:本题考查直角三角形30°角所对的直角边等于斜边的一半的性质,平行线的性质,三角形的内角和定理,熟记性质并求出△BCD是直角三角形是解题的关键.

练习册系列答案
相关题目
 24、如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
24、如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.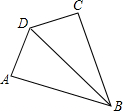 如图,已知:在四边形ABCD中,AD=DC=1,∠DCB=∠DAB=90°,BD=2,则四边形ABCD面积为
如图,已知:在四边形ABCD中,AD=DC=1,∠DCB=∠DAB=90°,BD=2,则四边形ABCD面积为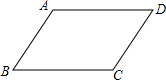 如图,已知:在四边形ABCD中,∠A=∠C,∠B+∠C=180°,求证:四边形ABCD是平行四边形.
如图,已知:在四边形ABCD中,∠A=∠C,∠B+∠C=180°,求证:四边形ABCD是平行四边形. 如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°,
如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°,