题目内容
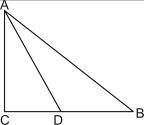
已知如下图,水厂A和工厂B、C正好构成等边△ABC,现由水厂A和B、C两厂供水,要在A、B、C间铺设输水管道,有如下四种设计方案,(图中实线为铺设管道路线),其中最合理的方案是( )


D
认真观察图形,其中只有O到A、B、C的距离相等,这样最节省材料,所以是最合理的方案.
解:设等边三角形的边长为a,
A、△ABC中的高线=AB?sin60°= ,故铺设路线的长度为AB+BC+
,故铺设路线的长度为AB+BC+ =2a+
=2a+ ;
;
B、△ABC中的高线=AB?sin60°= ,故铺设路线的长度为BC+
,故铺设路线的长度为BC+ =a+
=a+ ;
;
D、铺设路线的长为AP+BP+CP=3×a=3a;
C、铺设路线的长为AB+AC=2a.
因为2a+3a2>2a>a+3a2>3a,所以D中铺设路线最短.
故选D.
本题考查了等边三角形的性质;由于三角形内存在一点到三个顶点相等,所以类似最短路径问题,都涉及到三角形内这一点的运用.
解:设等边三角形的边长为a,
A、△ABC中的高线=AB?sin60°=
 ,故铺设路线的长度为AB+BC+
,故铺设路线的长度为AB+BC+ =2a+
=2a+ ;
;B、△ABC中的高线=AB?sin60°=
 ,故铺设路线的长度为BC+
,故铺设路线的长度为BC+ =a+
=a+ ;
;D、铺设路线的长为AP+BP+CP=3×a=3a;
C、铺设路线的长为AB+AC=2a.
因为2a+3a2>2a>a+3a2>3a,所以D中铺设路线最短.
故选D.
本题考查了等边三角形的性质;由于三角形内存在一点到三个顶点相等,所以类似最短路径问题,都涉及到三角形内这一点的运用.

练习册系列答案
相关题目
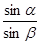 = .
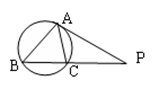
= .
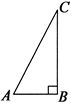
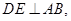 垂足是点E,
垂足是点E,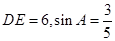 ,则菱形ABCD的周长是( )
,则菱形ABCD的周长是( ) 
 ,则这个三角形是
,则这个三角形是  ,迎水坡
,迎水坡 ,斜坡的坡度角为
,斜坡的坡度角为 ,则迎水坡的坡度是____________.
,则迎水坡的坡度是____________.

 长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为
长的直线型通道,中国馆位于世博轴的一侧(如下图所示). 现测得中国馆到世博轴两端的距离相等,并且从中国馆看世博轴两端的视角为 . 据此数据计算,求:中国馆到世博轴其中一端的距离是多少?.
. 据此数据计算,求:中国馆到世博轴其中一端的距离是多少?.
 中,
中, D是BC上的点,
D是BC上的点, .求AC(
.求AC( ,结果保留整数).
,结果保留整数).