题目内容
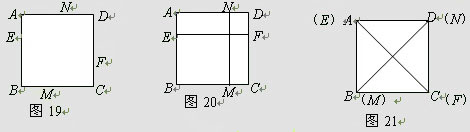
如图19,E、F、M、N是正方形ABCD四条边AB、BC、CD、DA上可以移动的四个点,每组对边上的两个点,可以连接成一条线段.
(1)如图20,如果EF∥BC,MN∥CD,那么EF MN(位置),EF MN(大小)
(2)如图21,如果E与A,F与C,M与B,N与D重合,那么EF MN(位置),EF MN(大小).
(3)当点E、F、M、N不再处于正方形ABCD四条边AB、BC、CD、DA特殊的位置时,猜想线段EF、MN满足什么位置关系时,才会有EF=MN,画出相应的图形,并证明你的猜想.
略
解析:(1)EF⊥MN,EF=MN;
(2)EF⊥MN,EF=MN;
(3)猜想:当EF⊥MN时,才会有EF=MN,如图,连接EF,作EF⊥MN.证明猜想:过点N作NG⊥BC,过点F作FH⊥AB,又EF⊥MN,在Rt△MNG和Rt△EFH中,∠MGN=∠EHF=90°,FH=NG,所以Rt△MNG≌ Rt△EFH,所以EF=MN

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目