题目内容
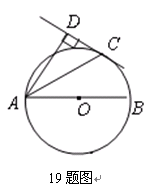
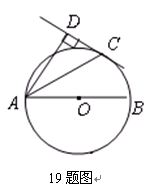
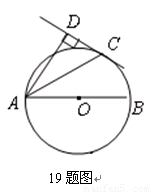
如图19,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D.锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.【小题1】求证:AC平分∠DAB
【小题2】过点O作线段AC的垂线OE,垂足为E(要求:尺规作图,保留作图痕迹,不写作法);
【小题3】若CD=4,AC=4,求垂线段OE的长.
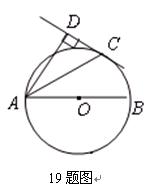
【小题1】连接OC,∵CD切⊙O于点C,∴OC⊥CD。
又∵AD⊥CD,∴OC∥AD。∴∠OCA=∠DAC。∵OC=OA,∴∠OCA=∠OAC。
∴∠OAC=∠DAC。∴AC平分∠DAB。 ………………………3分
【小题2】过点O作线段AC的垂线OE,如图所示:…………4分

【小题3】在Rt△ACD中,CD=4,AC=4,∴AD===8 。 ∵OE⊥AC,∴AE=AC=2。 ∵∠OAE=∠CAD ,∠AEO=∠ADC,∴△AEO∽△ADC。
∴=。∴OE=×CD=×4=
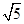 。即垂线段OE的长为
。即垂线段OE的长为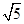 。…………8分 解析:
。…………8分 解析:(1)连接OC,由CD为圆O的切线,根据切线性质得到OC与CD垂直,又AD与CD垂直,根据平面上垂直于同一条直线的两直线平行得到AD与OC平行,由平行得一对内错角相等,又因为两半径OA与OC相等,根据等边对等角,得到一对相等的角,利用等量代换,即可得到∠DAC=∠OAC,即AC为∠DAB的平分线;
(2)以O为圆心,以大于O到AC的距离为半径画弧,与AC交于两点,分别以这两点为圆心,以大于这两点之间距离的一半长为半径在AC的另一侧画弧,两弧交于一点,经过此点与点O确定一条直线,即为所求的直线,如图所示;
(3)在直角三角形ACD中,由CD和AC的长,利用勾股定理求出AD的长,再根据垂径定理,由OE与AC 垂直,得到E为AC中点,求出AE的长,由(1)推出的角平分线得一对角相等,再由一对直角相等,根据两对对应角相等的两三角形相似,由相似得比例即可求出OE的长.

练习册系列答案
相关题目
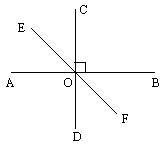 16、如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=128°19′,则∠BOF,∠AOF的度数分别为
16、如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=128°19′,则∠BOF,∠AOF的度数分别为