Question

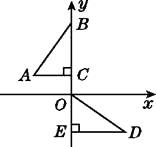
【题目】如图①,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.

（1）求证:BE=CE.
（2）如图②,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,AF=BF,原题设其他条件不变.求证:△AEF≌△BCF.

Answer 1

【答案】
（1）证明：∵AB=AC,D是BC的中点,∴∠BAE=∠CAE.
在△ABE和△ACE中, 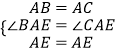∴△ABE≌△ACE(SAS).
∴BE=CE 。
（2）证明：∵AB=AC, 点D是BC的中点,
∴AD⊥BC.
∴∠EAF+∠C=90°.
∵BF⊥AC,
∴∠CBF+∠C=90°.
∴∠EAF=∠CBF.
在△AEF和△BCF中,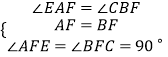
∴△AEF≌△BCF(ASA) 。
【解析】（1）根据等腰三角形的三线合一得出 ：∠BAE=∠CAE，然后利用SAS判断出△ABE≌△ACE ， 根据全等三角形对应边相等得出BE=CE ；
（2）根据等腰三角形的三线合一得出AD⊥BC，根据直角三角形两锐角互余得出∠EAF+∠C=90° ， ∠CBF+∠C=90°，根据同角的余角相等得出∠EAF=∠CBF，然后根据ASA判断出△AEF≌△BCF 。
【考点精析】解答此题的关键在于理解余角和补角的特征的相关知识，掌握互余、互补是指两个角的数量关系，与两个角的位置无关，以及对等腰三角形的性质的理解，了解等腰三角形的两个底角相等（简称：等边对等角）．