题目内容
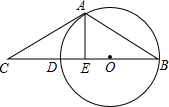 如图,过⊙O上一点A的切线AC与⊙O直径BD的延长线交于点C,过A作AE⊥BC于点E.
如图,过⊙O上一点A的切线AC与⊙O直径BD的延长线交于点C,过A作AE⊥BC于点E.(1)求证:∠CAE=2∠B;
(2)已知:AC=8,且CD=4,求⊙O的半径及线段AE的长.
分析:(1)连接OA,由切线的性质知:OA⊥AC,即∠OAC=90°,在Rt△OAC中,易证得∠CAE=∠AOE;而∠AOE是等腰△AOB的外角,即∠AOE=2∠B,等量代换后即可得出要证的结论;
(2)由切割线定理,易求得CB的长;即可求出BD和半径的长,Rt△CAO中,OA、OC的长已知,由勾股定理可求得AC的长,然后根据直角三角形面积的不同表示方程,即可求出AE的值.
(2)由切割线定理,易求得CB的长;即可求出BD和半径的长,Rt△CAO中,OA、OC的长已知,由勾股定理可求得AC的长,然后根据直角三角形面积的不同表示方程,即可求出AE的值.
解答: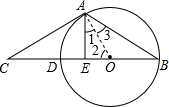 (1)证明:连接OA,
(1)证明:连接OA,
∵CA切⊙O于点A,
∴∠OAC=90°,即:∠CAE+∠1=90°.
又AE⊥BC,
∴∠2+∠1=90°.
∴∠CAE=∠2.
又OA=OB,
∴∠3=∠B,
∴∠2=2∠B,
∴∠CAE=2∠B.
(2)∵AC是⊙O的切线,
∴CA2=CD•CB.
∴CB=
=
=16.
∴⊙O的半径OB=
=6.
Rt△ACO中,CO=CD+DO=10,OA=6,
由勾股定理,得:AC=
=8.
又S△ACO=
AC•AO=
CO•AE.
∴AE=
=
=4.8.
 (1)证明:连接OA,
(1)证明:连接OA,∵CA切⊙O于点A,
∴∠OAC=90°,即:∠CAE+∠1=90°.
又AE⊥BC,
∴∠2+∠1=90°.
∴∠CAE=∠2.
又OA=OB,
∴∠3=∠B,
∴∠2=2∠B,
∴∠CAE=2∠B.
(2)∵AC是⊙O的切线,
∴CA2=CD•CB.
∴CB=
| CA2 |
| CD |
| 82 |
| 4 |
∴⊙O的半径OB=
| BC-CD |
| 2 |
Rt△ACO中,CO=CD+DO=10,OA=6,
由勾股定理,得:AC=
| OC2-OA2 |
又S△ACO=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=
| AC×AO |
| CO |
| 8×6 |
| 10 |
点评:本题主要考查了切线的性质及切割线定理,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
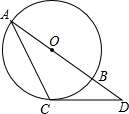 如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )
如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠D=40°,则∠A的度数为( )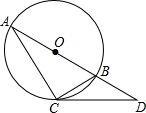 (2013•河东区二模)如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠CBD=α,则∠D的度数为
(2013•河东区二模)如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠CBD=α,则∠D的度数为