题目内容
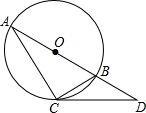 (2013•河东区二模)如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠CBD=α,则∠D的度数为
(2013•河东区二模)如图,过⊙O上一点C作⊙O的切线,交⊙O直径AB的延长线于点D.若∠CBD=α,则∠D的度数为270°-2α
270°-2α
(用含α的代数式表示)分析:根据三角形外角性质求出∠A,求出∠BCD=∠A,根据三角形内角和定理求出即可.
解答:解: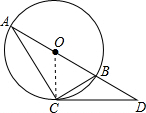
连接OC,
∵AB是⊙O直径,
∴∠ACB=90°,
∴∠A=∠CBD-∠ACB=α-90°,
∵∠ACB=90°,
∴∠A+∠ABC=90°,
∵CD是⊙O切线,
∴∠OCD=90°,
∴∠OCB+∠BCD=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠BCD=∠A=α-90°,
∴∠D=180°-∠CBD-∠BCD=180°-α-(α-90°)=270°-2α,
故答案为:270°-2α.

连接OC,
∵AB是⊙O直径,
∴∠ACB=90°,
∴∠A=∠CBD-∠ACB=α-90°,
∵∠ACB=90°,
∴∠A+∠ABC=90°,
∵CD是⊙O切线,
∴∠OCD=90°,
∴∠OCB+∠BCD=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠BCD=∠A=α-90°,
∴∠D=180°-∠CBD-∠BCD=180°-α-(α-90°)=270°-2α,
故答案为:270°-2α.
点评:本题考查了切线性质,圆周角定理,等腰三角形性质,三角形外角性质,三角形内角和定理的应用,关键是求出∠BCD的度数.

练习册系列答案
相关题目
 (2013•河东区二模)一个几何体如图所示,则该几何体的三视图是( )
(2013•河东区二模)一个几何体如图所示,则该几何体的三视图是( )