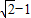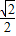题目内容
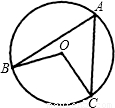
(2000•宁波)如图,圆内接四边形ABCD的两条对角线交于点P.已知AB=BC,CD= BD=1,设AD=x,用关于x的代数式表示PA与PC的积:PA•PC= .
BD=1,设AD=x,用关于x的代数式表示PA与PC的积:PA•PC= .
【答案】分析:根据相交弦定理,可得出PA•PC=BP•PD,那么可以转换成用x表示出BP,PD,那么可用相似三角形来求解,由题意可得:CD=1,BD=2,利用已知条件可以证明△ADB∽△PDC,根据相似三角形的性质得到CD:BD=PD:AD,而BD=2CD,这样就可以用x表示PD,BP,最后即可求出PA•PC与x的关系式.
解答:解:根据相交弦定理,可知PA•PC=BP•PD,
∵CD=1,BD=2
而AB=BC
∴
∴∠ADB=∠BDC
∵∠ABD=∠ACD
∴△ADB∽△PDC
∴CD:BD=PD:AD
而BD=2CD
∴PD= x
x
∴BP=BD-PD=2- x
x
∴PA•PC=BP•PD=(2- x)×
x)× x=-
x=- x2+x.
x2+x.
点评:本题主要考查了相交弦定理,圆周角定理以及相似三角形的判定和性质等知识点,根据相似三角形的性质求出相关的线段是解题的关键.
解答:解:根据相交弦定理,可知PA•PC=BP•PD,
∵CD=1,BD=2
而AB=BC
∴

∴∠ADB=∠BDC
∵∠ABD=∠ACD
∴△ADB∽△PDC
∴CD:BD=PD:AD
而BD=2CD
∴PD=
 x
x∴BP=BD-PD=2-
 x
x∴PA•PC=BP•PD=(2-
 x)×
x)× x=-
x=- x2+x.
x2+x.点评:本题主要考查了相交弦定理,圆周角定理以及相似三角形的判定和性质等知识点,根据相似三角形的性质求出相关的线段是解题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
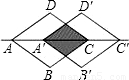
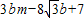 的值达到最小时,求BC的长.
的值达到最小时,求BC的长.
 ,若AC=
,若AC=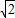 ,则菱形移动的距离AA′是( )
,则菱形移动的距离AA′是( )