题目内容
如图①,在矩形ABCD中,AB=12cm,AD=16cm,现将其按下列步骤折叠:(1)折叠矩形,使AB落在AD上,得到折痕AE,如图②;(2)将△AEB沿BE折叠,AE与DC交点F,如图③.则所得梯形BDFE的周长等于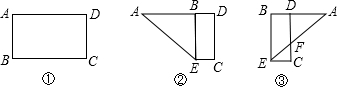
分析:先由折叠矩形,使AB落在AD上,得到折痕AE,由图性折叠的性质可求出BD、BE的长及∠AEB=45°,将△AEB沿BE折叠,AE与DC交点F,可利用相似三角形的性质求出DF的长,过F作FG⊥BE,则EG=GF,由勾股定理即可求出EF的长,进而可求出梯形BDFE的周长.
解答:解:∵AB=12cm,AD=16cm,
∴当矩形折叠后,AB落在AD上时,BD=AD-AB=16-4=4cm,BE=CD=12cm,∠AEB=45°,
如图③所示,
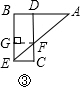
∵BE⊥AB,CD⊥AB,
∴△ADF∽△ABE,
∴
=
,
即
=
,
∴DF=8cm,
过F作FG⊥BE,则△EGF是等腰直角三角形,
GF=GE=BD=4,
∴EF=
=
=4
,
∴梯形BDFE的周长=BD+BE+DF+EF=4+12+8+4
=24+4
.
故答案为:24+4
.
∴当矩形折叠后,AB落在AD上时,BD=AD-AB=16-4=4cm,BE=CD=12cm,∠AEB=45°,
如图③所示,

∵BE⊥AB,CD⊥AB,
∴△ADF∽△ABE,
∴
| DF |
| BE |
| AD |
| AB |
即
| DF |
| 12 |
| 12-4 |
| 12 |
∴DF=8cm,
过F作FG⊥BE,则△EGF是等腰直角三角形,
GF=GE=BD=4,
∴EF=
| GF2+GE2 |
| 42+42 |
| 2 |
∴梯形BDFE的周长=BD+BE+DF+EF=4+12+8+4
| 2 |
| 2 |
故答案为:24+4
| 2 |
点评:本题考查的是图形的翻折变换,解答此题时要熟知翻折变换的性质,即折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
 24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是
24、如图,已知:AD是△ABC中BC边的中线,则S△ABD=S△ACD,依据是

 (2013•河北一模)如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止,设点P运动的路程为x,△ABP的面积为y,y关于x的函数图象如图2所示,则△ABC的面积是( )
(2013•河北一模)如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD运动至点D停止,设点P运动的路程为x,△ABP的面积为y,y关于x的函数图象如图2所示,则△ABC的面积是( )