题目内容
【题目】如图,AB是⊙O的直径,点D,E在⊙O上,∠A=2∠BDE,点C在AB的延长线上,∠C=∠ABD.
(1)求证:CE是⊙O的切线;
(2)若BF=2,EF=![]() ,求⊙O的半径长.
,求⊙O的半径长.
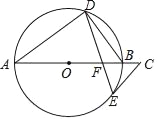
【答案】(1)见解析;(2)![]()
【解析】分析:(1)连接OE,首先得出△ABD∽△OCE,进而推出∠OCE=90°,即可得到结论;
(2)连接BE,得出△OBE∽△EBF,再利用相似三角形的性质得出OB的长,即可得到结论.
详解:(1)证明:连接OE,
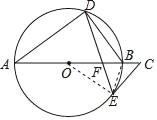
则∠BOE=2∠BDE,又∠A=2∠BDE,
∴∠BOE=∠A,
∵∠C=∠ABD,∠A=∠BOE,
∴△ABD∽△OCE
∴∠ADB=∠OEC,
又∵AB是直径,
∴∠OEC=∠ADB=90°
∴CE与⊙O相切;
(2)连接EB,则∠A=∠BED,
∵∠A=∠BOE,
∴∠BED=∠BOE,
在△BOE和△BEF中,
∠BEF=∠BOE,∠EBF=∠OBE,
∴△OBE∽△EBF,
∴![]() ,则
,则![]() ,
,
∵OB=OE,
∴EB=EF,
∴![]() ,
,
∵BF=2,EF=![]() ,
,
∴![]() ,
,
∴OB=![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目