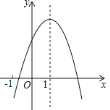题目内容
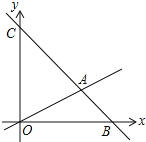
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,动点
,动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动.
上运动.
(1)求直线![]() 的解析式.
的解析式.
(2)求![]() 的面积.
的面积.
(3)是否存在点![]() ,使
,使![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ?若存在求出此时点
?若存在求出此时点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
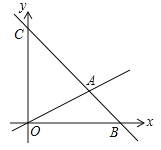
【答案】(1)y=-x+6;(2)12;(3)M1(2,1)或M2(2,4)或M3(-2,8).
【解析】
(1)利用待定系数法即可求得函数的解析式;
(2)求得C的坐标,即OC的长,利用三角形的面积公式即可求解;
(3)当△OMC的面积是△OAC的面积的![]() 时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
时,根据面积公式即可求得M的横坐标,然后代入解析式即可求得M的坐标.
解:(1)设直线AB的解析式是y=kx+b,
根据题意得![]() ,
,
解得:![]() ,
,
则直线的解析式是:y=-x+6;
(2)在y=-x+6中,令x=0,解得:y=6,
S△OAC=![]() ×6×4=12;
×6×4=12;
(3)设OA的解析式是y=mx,则4m=2,
解得:m=![]() ,
,
则直线的解析式是:y=![]() x,
x,
∵当△OMC的面积是△OAC的面积的![]() 时,
时,
又∵动点![]() 在线段
在线段![]() 和射线
和射线![]() 上运动
上运动
∴①当M的横坐标是![]() ×4=2,
×4=2,
在y=![]() x中,当x=2时,y=1,则M的坐标是(2,1);
x中,当x=2时,y=1,则M的坐标是(2,1);
在y=-x+6中,x=2则y=4,则M的坐标是(2,4).
则M的坐标是:M1(2,1)或M2(2,4).
②当M的横坐标是:-2,
在y=-x+6中,当x=-2时,y=8,则M的坐标是(-2,8);
综上所述:M的坐标是:M1(2,1)或M2(2,4)或M3(-2,8).

练习册系列答案
相关题目