Question

【题目】已知抛物线经过A（3，0）、B（4，1）两点，且与y轴交于点C．

（1）求抛物线的解析式；

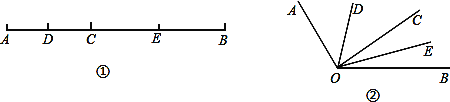
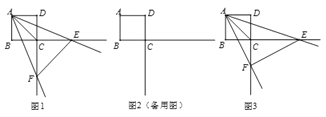
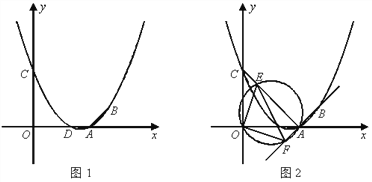
（2）如图1，设抛物线与x轴的另一个交点为D，在抛物线的对称轴上找一点H，使△CDH的周长最小，求出H点的坐标并求出最小周长值；

（3）如图2，连接AC，E为线段AC上任意一点（不与A、C重合），经过A、E、O三点的圆交直线AB于点F，当△OEF的面积取得最小值时，求面积的最小值及E点坐标。

Answer 1

【答案】（1）求抛物线的解析式为；

（2）H点的坐标(， ) ，最小周长值是

（3）面积的最小值为，E点坐标为（， ）.

【解析】试题分析：（1）把点A（3，0），B（4，1）的坐标代入抛物线解析式，利用待定系数法求二次函数解析式；（2）如图1中，连接DC、AC，AC交对称轴于H，连接DH，此时△CDH的周长最小．（3）如图2中，作BD⊥OA于D．首先证明△EOF是等腰直角三角形，当OE⊥AC时，△EOF的面积最小．

试题解析：（1）∵抛物线y=ax2+bx+3（a≠0）经过A（3，0），B（4，1）两点，

解得： ，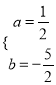

∴

(2)∴点C的坐标为：（0，3）；

容易求出D（2，0）

对称轴为

A、D两点是对称点，

连接AC交对称轴于H，连接CD,DH

此时△CDH的周长最小

C（0，3），A （3，0）

当时， H(,)

CD+DH+CH=CD+CH+HA=CD+AC=

（3）如图3：作EM⊥AO于M，

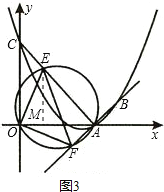
∵直线AB的解析式为：y=x-3，

∴易证得∠OAF=45°，

∵OC=OA=3

∴∠OAC=45°，

∴∠OAC=∠OAF=45°，

∴AC⊥AF

∴∠EAF=90°

∴EF是圆的直径

∴∠EOF＝=90°∠OFE=∠OAC=45°

∴△OEF是等腰直角三角形

∴，

∴当OE最小时最小，

∵OE⊥AC时OE最小，又∵AC=OA=3

∴CE=EA

∴OE=，

∴=

又∵E是AC的中点

∴E（， ）