题目内容
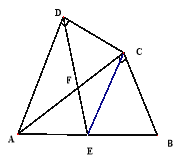
【题目】如图1,□ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形 ABCD 是菱形;
(2)若∠ADC=60°,BE=2,求BD的长.

【答案】(1)见详解;(2)![]() .
.
【解析】
(1)首先根据平行四边形的性质和已知条件推出四边形OAEB是矩形,从而得出OA⊥OB,即可得证;
(2)由(1)得四边形OAEB是矩形,四边形ABCD是菱形,从而推出OA=BE=2,∠ODA=∠ODC=30°,由此可得在Rt△OAD中,OD=![]() ,即可得出BD.
,即可得出BD.
(1)∵四边形ABCD是平行四边形,
∴AB=CD,
∵OE=CD,
∴AB=OE,
∵AE∥BD,BE∥AC,
∴四边形OAEB是平行四边形,
∴四边形OAEB是矩形,
∴OA⊥OB,
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形;
(2)由(1)可知四边形OAEB是矩形,
∴OA=BE=2,
由(1)得四边形ABCD是菱形,
∴∠ODA=∠ODC,AC⊥BD,
又∵∠ADC=60°,
∴∠ODA=∠ODC=30°,
∴在Rt△OAD中,OD=![]() =
=![]() =
=![]() ,
,
∴BD=2OD=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】(5分)(2015春鞍山期末)小王某月手机话费中的各项费用统计情况见下列图表,请你根据图表信息完成下列各题:
项目 | 月功能费 | 基本话费 | 长途话费 | 短信费 |
金额/元 | 5 | 50 |
(1)请将表格补充完整;
(2)请将条形统计图补充完整;
(3)扇形统计图中,表示短信费的扇形的圆心角是多少度?