题目内容
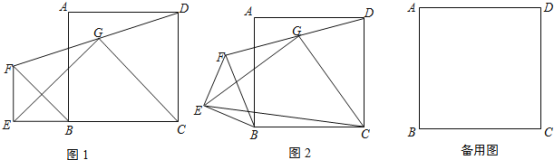
【题目】四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G为DF的中点,连接EG,CG,EC.
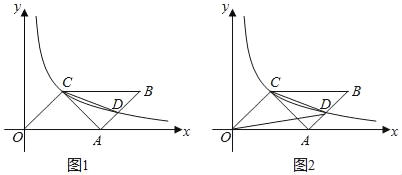
(1)如图1,若点E在CB边的延长线上,直接写出EG与GC的位置关系及![]() 的值;
的值;
(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
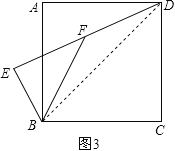
(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,![]() ,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
,当E,F,D三点共线时,求DF的长及tan∠ABF的值.
【答案】(1)EG⊥CG,![]() ;(2)结论还成立,证明见解析;
;(2)结论还成立,证明见解析;
【解析】
试题(1)过G作GH⊥EC于H,推出EF∥GH∥DC,求出H为EC中点,根据梯形的中位线求出EG=GC,GH=![]() (EF+DC)=
(EF+DC)=![]() (EB+BC),推出GH=EH=BC,根据直角三角形的判定推出△EGC是等腰直角三角形即可.
(EB+BC),推出GH=EH=BC,根据直角三角形的判定推出△EGC是等腰直角三角形即可.
(2)延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,证△EFG≌△HDG,推出DH=EF=BE,∠FEG=∠DHG,求出∠EBC=∠HDC,证出△EBC≌△HDC,推出CE=CH,∠BCE=∠DCH,求出△ECH是等腰直角三角形,即可得出答案.
(3)连接BD,求出![]() ,推出∠DBE=60°,求出∠ABF=30°,解直角三角形求出即可.
,推出∠DBE=60°,求出∠ABF=30°,解直角三角形求出即可.
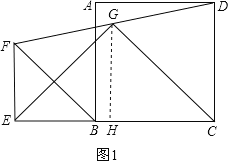
试题解析:(1)EG⊥CG,![]() ,理由是:
,理由是:
如图1,过G作GH⊥EC于H,
∵∠FEB=∠DCB=90°,∴EF∥GH∥DC.
∵G为DF中点,∴H为EC中点.
∴EG=GC,GH=![]() (EF+DC)=
(EF+DC)=![]() (EB+BC),即GH=EH=BC.
(EB+BC),即GH=EH=BC.
∴∠EGC=90°,即△EGC是等腰直角三角形.
∴![]()
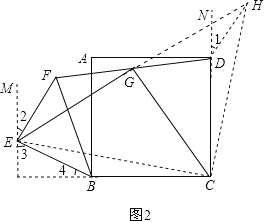
(2)结论还成立,证明如下:
如图2,延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,
∵在△EFG和△HDG中,GF=GD,∠FGE=∠DGH,EG=HG,∴△EFG≌△HDG(SAS).
∴DH=EF=BE,∠FEG=∠DHG.∴EF∥DH.
∴∠1=∠2=90°-∠3=∠4.∴∠EBC=180°-∠4=180°-∠1=∠HDC.
在△EBC和△HDC中,BE=DH,∠EBC=∠HDC,BC=CD,∴△EBC≌△HDC.
∴CE=CH,∠BCE=∠DCH.
∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°.
∴△ECH是等腰直角三角形,
∵G为EH的中点,
∴EG⊥GC,![]() ,即(1)中的结论仍然成立.
,即(1)中的结论仍然成立.
(3)如图3,连接BD,
∵AB=![]() ,正方形ABCD,∴BD=2.∴
,正方形ABCD,∴BD=2.∴![]() .
.
∴∠DBE=60°.∴∠ABE=∠DBE-∠ABD=15°.∴∠ABF=45°-15°=30°.
∴![]() .∴DE=
.∴DE=![]() BE=
BE=![]() .
.
∴DF=DE-EF=![]() .
.