题目内容
【题目】如图,已知正方形ABCD的边长是5,点O在AD上,且⊙O的直径是4.
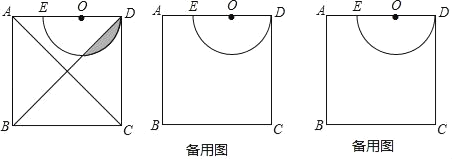
(1)正方形的对角线BD与半圆O交于点F,求阴影部分的面积;
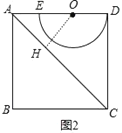
(2)利用图判断,半圆O与AC有没有公共点,说明理由.(提示:![]() ≈1.41)
≈1.41)
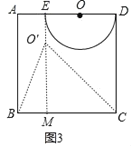
(3)将半圆O以点E为中心,顺时针方向旋转.
①旋转过程中,△BOC的最小面积是 ;
②当半圆O过点A时,半圆O位于正方形以外部分的面积是 .
【答案】(1)π﹣2;(2)半圆O与AC没有公共点.理由见解析;(3)①![]() ;②2π﹣
;②2π﹣![]() .
.
【解析】
(1)连接OF,如图1,先证明△ODF为等腰直角三角形得到∠DOF=90°,如何根据扇形面积公式,利用S阴影部分=S扇形DOF-S△DOF进行计算;
(2)如图2,作OH⊥AC于H,先证明△OAH为等腰直角三角形,则OH=![]() OA≈2.13,然后比较OH与半径的大小关系可判断半圆O与AC的位置关系;
OA≈2.13,然后比较OH与半径的大小关系可判断半圆O与AC的位置关系;
(3)①如图3,作EM⊥BC于M,当点O到BC的距离最小,此时△ABC的面积最小,易得点O到BC的最小距离为3,然后根据三角形面积公式计算;
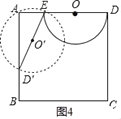
②当半圆O过点A时,根据圆周角定理的推论可判定点D落在AB上的点D′处,如图4,利用勾股定理计算出AD′=![]() ,然后利用半圆面积减去△AED′的面积即可得到半圆O位于正方形以外部分的面积.
,然后利用半圆面积减去△AED′的面积即可得到半圆O位于正方形以外部分的面积.
(1)连接OF,如图1,
∵四边形ABCD为正方形,
∴∠ADB=45°,
∵OF=OD,
∴△ODF为等腰直角三角形,
∴∠DOF=90°,
∴S阴影部分=S扇形DOF﹣S△DOF=![]() ﹣
﹣![]() ×2×2=π﹣2;
×2×2=π﹣2;
(2)半圆O与AC没有公共点.理由如下:
如图2,作OH⊥AC于H,
∵四边形ABCD为正方形,
∴∠DAC=45°,
∴△OAH为等腰直角三角形,
∴OH=![]() OA=
OA=![]() ×3≈2.13,
×3≈2.13,
∵OH>2,
∴AC与半圆O相离,
即半圆O与AC没有公共点;
(3)①如图3,作EM⊥BC于M,
当点O落在EM上的O′处时,点O到BC的距离最小,此时△ABC的面积最小,
所以△BOC的最小面积=![]() ×5×(5﹣2)=
×5×(5﹣2)=![]() ;
;
②当半圆O过点A时,即点A在半圆上,而∠A=90°,
所以点D落在AB上的点D′处,如图4,
在Rt△AED′中,AD′=![]() =
=![]() =
=![]() ,
,
所以半圆O位于正方形以外部分的面积=![]() π22﹣
π22﹣![]() =2π﹣
=2π﹣![]() .
.
故答案为![]() ;2π﹣
;2π﹣![]() .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】已知一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 0 | p | m | 3 |
| q | 0 | … |
(1)求这个二次函数的表达式;
(2)表格中字母m= ;(直接写出答案)
(3)在给定的直角坐标系中,画出这个二次函数的图象;
(4)以上二次函数的图象与x轴围成的封闭区域内(不包括边界),横、纵坐标都是整数的点共有 个.(直接写出结果)
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.