题目内容
等腰三角形一边长为2,周长为5,则它的腰长为
- A.2
- B.1.5
- C.1
- D.1.5或2
D
分析:分别从若等腰三角形的腰长为2与若等腰三角形的底边长为2去分析求解即可求得答案.
解答:若等腰三角形的腰长为2,
则底边长为:5-2-2=1,
∵2+1>2,
能组成三角形,
此时它的腰长为2;
若等腰三角形的底边长为2,
则腰长为: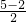 =1.5,
=1.5,
∵1.5+1.5>2,
能组成三角形,
此时它的腰长为1.5.
∴它的腰长为1.5或2.
故选D.
点评:此题考查了等腰三角形的性质以及三角形的三边关系.此题难度不大,注意掌握分类讨论思想的应用.
分析:分别从若等腰三角形的腰长为2与若等腰三角形的底边长为2去分析求解即可求得答案.
解答:若等腰三角形的腰长为2,
则底边长为:5-2-2=1,
∵2+1>2,
能组成三角形,
此时它的腰长为2;
若等腰三角形的底边长为2,
则腰长为:
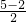 =1.5,
=1.5,∵1.5+1.5>2,
能组成三角形,
此时它的腰长为1.5.
∴它的腰长为1.5或2.
故选D.
点评:此题考查了等腰三角形的性质以及三角形的三边关系.此题难度不大,注意掌握分类讨论思想的应用.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目