题目内容
已知三角形的周长是c,其中一边是另一边2倍,则三角形的最小边的范围是
- A.
 与
与 之间
之间 - B.
 与
与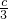 之间
之间 - C.
 与
与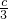 之间
之间 - D.
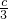 与
与 之间
之间
A
分析:根据题意,设一边是a,一边是2a,那么另一边最大不超过3a,最小不小于a,那么最小边是a,然后结合周长定义解不等式组从而可得三角形的最小边的范围.
解答:因为最小边为a,一边为2a,所以另一边A:a<A<3a(三角形两边之和大于第三边三角形两边之差小于第三边)
所以4a<c<6a,
所以三角形的最小边的范围是 与
与 之间.
之间.
故选A.
点评:本题考查了三角形的三边关系.注意分类讨论.
分析:根据题意,设一边是a,一边是2a,那么另一边最大不超过3a,最小不小于a,那么最小边是a,然后结合周长定义解不等式组从而可得三角形的最小边的范围.
解答:因为最小边为a,一边为2a,所以另一边A:a<A<3a(三角形两边之和大于第三边三角形两边之差小于第三边)
所以4a<c<6a,
所以三角形的最小边的范围是
 与
与 之间.
之间.故选A.
点评:本题考查了三角形的三边关系.注意分类讨论.

练习册系列答案
相关题目
已知三角形的周长是c,其中一边是另一边2倍,则三角形的最小边的范围是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 ,其中一边是另一边2倍,则三角形的最小边的范围是( )
,其中一边是另一边2倍,则三角形的最小边的范围是( ) 与
与 之间 (B)
之间 (B) 之间
之间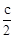 之间
之间