题目内容
【题目】正方形的A1B1P1P2顶点P1、P2在反比例函数y= 
（x＞0）的图象上，顶点A1、B1分别在x轴、y轴的正半轴上，再在其右侧作正方形P2P3A2B2 ， 顶点P3在反比例函数y= （x＞0）的图象上，顶点A2在x轴的正半轴上，则点P3的坐标为 ．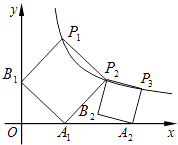 
【答案】（ 
+1， ﹣1）
【解析】解：作P1C⊥y轴于C，P2D⊥x轴于D，P3E⊥x轴于E，P3F⊥P2D于F，如图，
设P1（a， 
），则CP1=a，OC= ，
∵四边形A1B1P1P2为正方形，
∴Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D，
∴OB1=P1C=A1D=a，
∴OA1=B1C=P2D= ﹣a，
∴OD=a+ ﹣a= ，
∴P2的坐标为（ ， ﹣a），
把P2的坐标代入y= 
（x＞0），得到（ ﹣a） =2，解得a=﹣1（舍）或a=1，
∴P2（2，1），
设P3的坐标为（b， 
），
又∵四边形P2P3A2B2为正方形，
∴Rt△P2P3F≌Rt△A2P3E，
∴P3E=P3F=DE= ，
∴OE=OD+DE=2+ ，
∴2+ =b，解得b=1﹣ （舍），b=1+ ，
∴ = 
= ﹣1，
∴点P3的坐标为 （ +1， ﹣1）．
故答案为：（ +1， ﹣1）．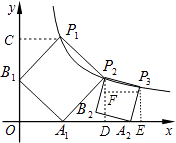
作P1C⊥y轴于C，P2D⊥x轴于D，P3E⊥x轴于E，P3F⊥P2D于F，设P1（a， ），则CP1=a，OC= ，易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D，则OB1=P1C=A1D=a，所以OA1=B1C=P2D= ﹣a，则P2的坐标为（ ， ﹣a），然后把P2的坐标代入反比例函数y= ，得到a的方程，解方程求出a，得到P2的坐标；设P3的坐标为（b， ），易得Rt△P2P3F≌Rt△A2P3E，则P3E=P3F=DE= ，通过OE=OD+DE=2+ =b，这样得到关于b的方程，解方程求出b，得到P3的坐标．
