题目内容
 如图,AD=8cm,CD=6cm,AD⊥CD,BC=24cm,AB=26cm,求图形的面积.
如图,AD=8cm,CD=6cm,AD⊥CD,BC=24cm,AB=26cm,求图形的面积.考点:勾股定理,勾股定理的逆定理
专题:
分析:先连接AC,在Rt△ACD中,AD=8cm,CD=6cm,可求出AC;在△ABC中,由勾股定理的逆定理可证△ABC为直角三角形,利用两个直角三角形的面积差求图形的面积.
解答: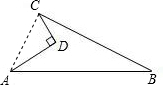 解:连接AC,在Rt△ACD中,AD=8cm,CD=6cm,
解:连接AC,在Rt△ACD中,AD=8cm,CD=6cm,
∴AC=
=
=10cm,
在△ABC中,
∵AC2+BC2=102+242=262=AB2,
∴△ABC为直角三角形;
∴图形面积为:
S△ABC-S△ACD=
×10×24-
×6×8=96cm2.
故图形的面积为96cm2.
 解:连接AC,在Rt△ACD中,AD=8cm,CD=6cm,
解:连接AC,在Rt△ACD中,AD=8cm,CD=6cm,∴AC=
| AD2+CD2 |
| 82+62 |
在△ABC中,
∵AC2+BC2=102+242=262=AB2,
∴△ABC为直角三角形;
∴图形面积为:
S△ABC-S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
故图形的面积为96cm2.
点评:本题主要考查了勾股定理及其逆定理的运用,三角形面积的求法.关键是做出辅助线,构造直角三角形,掌握勾股定理与逆定理.

练习册系列答案
相关题目
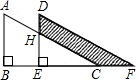 如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积.
如图,两个大小一样的直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积.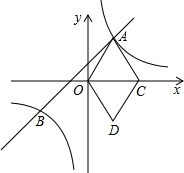 如图,在平面直角坐标系xOy中,直线y=mx+1与双曲线
如图,在平面直角坐标系xOy中,直线y=mx+1与双曲线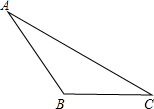 按要求画图,并描述所作线段.
按要求画图,并描述所作线段.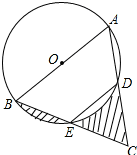 如图,AB是⊙O的直径,AB=4,∠BED=120°,DE∥AB,则图中阴影部分的面积之和为
如图,AB是⊙O的直径,AB=4,∠BED=120°,DE∥AB,则图中阴影部分的面积之和为