题目内容
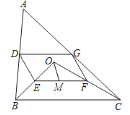
【题目】如图,点![]() 是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点
是ΔABC内一点,连接OB、OC,并将AB、OB、OC、AC的中点![]() 、
、![]() 、
、![]() 、
、![]() 依次连结,得到四边形
依次连结,得到四边形![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若![]() 为
为![]() 的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
的中点,OM=5,∠OBC与∠OCB互余,求DG的长度.
【答案】(1)见解析;(2)10.
【解析】
(1)根据三角形的中位线性质求出DG∥BC,EF∥BC,DG=![]() BC,EF=
BC,EF=![]() BC,求出DG∥EF,DG=EF,根据平行四边形的判定得出即可;
BC,求出DG∥EF,DG=EF,根据平行四边形的判定得出即可;
(2)求出∠BOC=90°,根据直角三角形的斜边上中线性质得出EF=2OM,即可求出答案.
(1)证明: ∵点D、E、F、G分别是AB、OB、OC、AC的中点,
∴DG∥BC,EF∥BC,DG=![]() BC,EF=
BC,EF=![]() BC,
BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)解:由 (1)知:四边形DEFG是平行四边形,
∴DG=EF.
∵ ∠OBC与∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°.
∵M为EF的中点,OM=5,
∴OM=![]() EF,即EF=2OM=2×5=10,
EF,即EF=2OM=2×5=10,
∴DG=10.

练习册系列答案
相关题目