题目内容
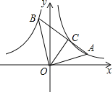
【题目】如图,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 在反比例函数
在反比例函数![]() 的图象上,且
的图象上,且![]() .线段
.线段![]() 交反比例函数
交反比例函数![]() 的图象于另一点
的图象于另一点![]() ,连接OC,若点
,连接OC,若点![]() 为
为![]() 的中点,则
的中点,则![]() 的值为________.
的值为________.
【答案】![]()
【解析】
过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,根据点
,根据点![]() 为
为![]() 的中点即可找出点
的中点即可找出点![]() 的坐标,再结合相似三角形的性质即可得出
的坐标,再结合相似三角形的性质即可得出![]() 、
、![]() 的关系,结合点在反比例函数的性质即可得出关于
的关系,结合点在反比例函数的性质即可得出关于![]() 、
、![]() 的二元二次方程,解方程组求出
的二元二次方程,解方程组求出![]() 、
、![]() 的值,进而即可得出点
的值,进而即可得出点![]() 、
、![]() 的坐标,利用正切的定义结合等边三角形的判定即可得出
的坐标,利用正切的定义结合等边三角形的判定即可得出![]() 为等边三角形,由此即可得出结论
为等边三角形,由此即可得出结论
过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,如图所示.
,如图所示.

设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
∵![]() ,
,
∴  ,即
,即![]() ①.
①.
∵点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ,即
,即![]() ②.
②.
联立①②成方程组,解得: 或
或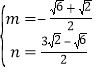 (舍去),
(舍去),
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
故答案为:![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目