题目内容
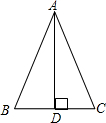 如图,已知在等腰三角形ABC中,底边BC=18,
如图,已知在等腰三角形ABC中,底边BC=18,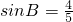 ,求出底边上的高AD的长?
,求出底边上的高AD的长?
解:∵等腰三角形ABC中,底边BC=18,
∴BD=CD=9,
∵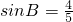 ,
,
∴设AD=4x,AB=5x,
∴(4x)2+92=(5x)2,
解得x=3,
∴AD=4x=12.
分析:利用等腰三角形的性质求出BD的长,然后利用解直角三角形的知识求AD的长即可.
点评:本题考查了解直角三角形和等腰三角形的性质,解题过程中应用了方程思想.
∴BD=CD=9,
∵
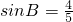 ,
,∴设AD=4x,AB=5x,
∴(4x)2+92=(5x)2,
解得x=3,
∴AD=4x=12.
分析:利用等腰三角形的性质求出BD的长,然后利用解直角三角形的知识求AD的长即可.
点评:本题考查了解直角三角形和等腰三角形的性质,解题过程中应用了方程思想.

练习册系列答案
相关题目
 互唯一确定的.
互唯一确定的.
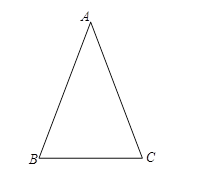
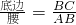 ,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题: ,S△ABC=24,求△ABC的周长.
,S△ABC=24,求△ABC的周长.