��Ŀ����
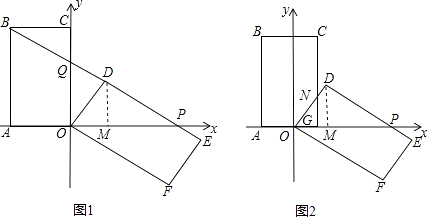
����Ŀ����֪����OABC�У�OA=3��AB=6����OA��OC���ڵ�ֱ��Ϊ�����ᣬ������ͼ1��ƽ��ֱ������ϵ��������OABC�Ƶ�O˳ʱ�뷽����ת���õ�����ODEF������B��ֱ��DE��ʱ����ֱ��DE��x�ύ�ڵ�P����y�ύ�ڵ�Q��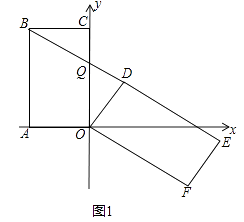
��1����֤����BCQ�ա�ODQ��
��2�����P�����ꣻ
��3����������OABC����ƽ�ƣ�ͼ2�����õ�����ABCG�������ABCG�����ODEF�ص����ֵ����ΪS��OG=x����ֱ��д��x��3ʱ��S��x֮��ĺ�����ϵʽ������д���Ա���x��ȡֵ��Χ��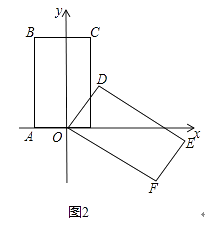
���𰸡�
��1��
֤�������ı���OABC���ı���ODEF�Ǿ��Σ�
���BCQ=��ODE=��ODQ=90�㣬BC=OD=3��
���ڡ�BCQ�͡�ODQ��
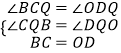
���BCQ�ա�ODQ��
��2��
�⣺�ߡ�BCQ�ա�ODQ��
��CQ=DQ��
��Rt��ODQ�У���ODQ=90�㣬OD=3���ɹ��ɶ����ã�OQ2=OD2+DQ2��
��OQ2=��6��OQ��2+32��
��ã�OQ= ![]() ��DQ=
��DQ= ![]() ��
��
��Q�������ǣ�0�� ![]() ����
����
�߾���ABCO�ı�AB=6��OA=3��
��B�������ǣ���3��6����
��ֱ��BD�Ľ���ʽ��y=kx+ ![]() ��
��
��B���������ã�k=�� ![]() ��
��
��ֱ��BD�Ľ���ʽ��y=�� ![]() x+
x+ ![]() ��
��
��y=0������ ![]() x+
x+ ![]() =0��
=0��
��ã�x=5��
��P�������ǣ�5��0����
��3��
�⣺
��D��DM��OP��M����ͼ1��
�ߡ�DMO=��ODQ=90�㣬OQ��DM��
���QOD=��MDO��
���QDO�ס�OMD��
�� ![]() =
= ![]() =
= ![]() ��
��
�� ![]() =
= ![]() =
= ![]() ��
��
���ã�OM= ![]() ��DM=
��DM= ![]() ��
��
OG=x��x��3��
��Ϊ�������������ͼ2����0��x�� ![]() ʱ��
ʱ��
��DM= ![]() ��OM=
��OM= ![]() ��OG=x��CG��DM��
��OG=x��CG��DM��
���ONG�ס�ODM��
�� ![]() =
= ![]() ��
��
NG= ![]() x��
x��
��S= ![]() ��OG��GN=
��OG��GN= ![]() x
x ![]() x��
x��
S= ![]() x2��
x2��
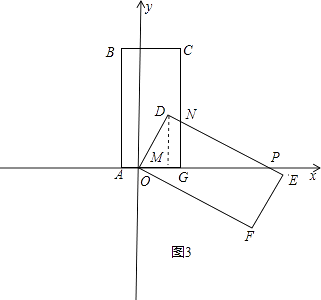
����ͼ3���� ![]() ��x��3ʱ��
��x��3ʱ��
��Rt��ODP�У��ɹ��ɶ����ã�PD= ![]() =4��
=4��
��DM= ![]() ��OM=
��OM= ![]() ��
��
��PM=5�� ![]() =
= ![]() ��
��
��OG=x��CG��DM��
���PGN�ס�PMD��
�� ![]() =
= ![]() ��
��
��NG= ![]() ��5��x����
��5��x����
��S=S��ADP��S��PGN= ![]() ��3��4��
��3��4�� ![]() ��5��x��
��5��x�� ![]() ��5��x����
��5��x����
S=�� ![]() x2+
x2+ ![]() x��
x�� ![]() ��
��
��S��x�ĺ�����ϵʽ��S= ![]() x2��0��x��
x2��0��x�� ![]() ����S=��
����S=�� ![]() x2+
x2+ ![]() x��
x�� ![]() ��
�� ![]() ��x��3����
��x��3����
����������1���������������ʵó���BCQ=��ODE=��ODQ=90�㣬BC=OD=3������ȫ�������ε��ж��Ƴ����ɣ���2������ȫ�ȵó�CQ=DQ����Rt��ODQ���ɹ��ɶ����ó�OQ2=��6��OQ��2+32 �� ���OQ= ![]() ��DQ=
��DQ= ![]() ���ó�Q�������ǣ�0��
���ó�Q�������ǣ�0�� ![]() �������ֱ��BD�Ľ���ʽ�����ɵó��𰸣���3����D��DM��OP��M�����OM��DM����Ϊ�������������ͼ�Σ����GN�����������ε������ʽ������ɣ�
�������ֱ��BD�Ľ���ʽ�����ɵó��𰸣���3����D��DM��OP��M�����OM��DM����Ϊ�������������ͼ�Σ����GN�����������ε������ʽ������ɣ�
�����㾫�������ڱ��⿼���ƽ���ı��ε����ʺ�ƽ���ı��ε��ж�����Ҫ�˽�ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣�����Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı��β��ܵó���ȷ�𰸣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�