题目内容
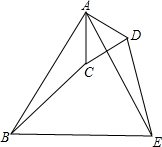 如图,将△ABC绕点A逆时针旋转60度后得到△AED,连接BE,CD,若∠BAC=30°,则下列说法:①BC=ED;②△ABE和△ACD都是正三角形;③∠CAE=30°;④AE⊥CD.其中正确的说法是
如图,将△ABC绕点A逆时针旋转60度后得到△AED,连接BE,CD,若∠BAC=30°,则下列说法:①BC=ED;②△ABE和△ACD都是正三角形;③∠CAE=30°;④AE⊥CD.其中正确的说法是
- A.①
- B.①②
- C.①②③
- D.①②③④
D
分析:分别根据图形旋转的性质、等边三角形的判定与性质对各小题进行逐一判断即可.
解答:∵△AED由△ABC旋转而成,
∴BC=DE,故①正确;
∵将△ABC绕点A逆时针旋转60度后得到△AED,
∴∠BAE=60°,AB=AE,
∴△ABE是正三角形;
同理,∠CAD=60°,AC=AD,
∴△ACD是正三角形,故②正确;
∵∠BAE=60°,∠BAC=30°,
∴∠CAE=30°,故③正确;
∵△ACD是等边三角形,∠CAE=30°,
∴AE是∠CAD的平分线,
∴AE⊥CD,故④正确.
故选D.
点评:本题考查的是图形旋转的性质及等边三角形的判定定理,熟知图形旋转后所得图形与原图形全等的性质是解答此题的关键.
分析:分别根据图形旋转的性质、等边三角形的判定与性质对各小题进行逐一判断即可.
解答:∵△AED由△ABC旋转而成,
∴BC=DE,故①正确;
∵将△ABC绕点A逆时针旋转60度后得到△AED,
∴∠BAE=60°,AB=AE,
∴△ABE是正三角形;
同理,∠CAD=60°,AC=AD,
∴△ACD是正三角形,故②正确;
∵∠BAE=60°,∠BAC=30°,
∴∠CAE=30°,故③正确;
∵△ACD是等边三角形,∠CAE=30°,
∴AE是∠CAD的平分线,
∴AE⊥CD,故④正确.
故选D.
点评:本题考查的是图形旋转的性质及等边三角形的判定定理,熟知图形旋转后所得图形与原图形全等的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 5、如图,将△ABC绕点A旋转到△AB1C1,下列说法正确的个数有( )
5、如图,将△ABC绕点A旋转到△AB1C1,下列说法正确的个数有( ) 8、在△ABC中,∠ACB=90°,∠A=20°,如图,将△ABC绕点C按逆时针方向旋转角α到∠A′C′B′的位置,其中A′,B′分别是A、B的对应点,B在A′B′上,CA′交AB于D,则∠BDC的度数为( )
8、在△ABC中,∠ACB=90°,∠A=20°,如图,将△ABC绕点C按逆时针方向旋转角α到∠A′C′B′的位置,其中A′,B′分别是A、B的对应点,B在A′B′上,CA′交AB于D,则∠BDC的度数为( )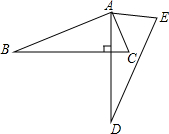 (2013•南昌)如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )
(2013•南昌)如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,∠BAC的度数为( )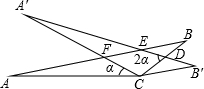 (2013•南岗区一模)如图,将△ABC绕点C顺时针方向旋转a得△A′B′C,A′B′与BC交于D,与AB交于E,A′C与AB交于F,若∠A′DC=2a,AC=3,AF=2,则BF的长是
(2013•南岗区一模)如图,将△ABC绕点C顺时针方向旋转a得△A′B′C,A′B′与BC交于D,与AB交于E,A′C与AB交于F,若∠A′DC=2a,AC=3,AF=2,则BF的长是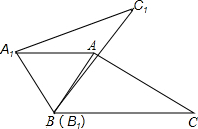 如图,将△ABC绕点B旋转到△A1B1C1的位置时,AA1∥BC,∠ABC=70°,则∠CBC1=
如图,将△ABC绕点B旋转到△A1B1C1的位置时,AA1∥BC,∠ABC=70°,则∠CBC1=