Question

【题目】四边形ABCD为菱形，点P为对角线BD上的一个动点.

（1）如图1，连接AP并延长交BC的延长线于点E，连接 PC，求证：∠AEB=∠PCD.

（2）如图1，当PA=PD且PC⊥BE时，求∠ABC的度数.

（3）连接AP并延长交射线BC于点E，连接 PC，若∠ABC=90°且ΔPCE是等腰三角形，求得∠PEC的度数 （第（3）问 直接写出结果，不写过程）

Answer 1

【答案】（1）证明见解析；（2）60°；（3）30°或120°

【解析】试题分析：（1）利用菱形的性质，易得∠PDA=∠PDC，AD=CD，利用SAS定理证得△PAD≌△PCD，由全等三角形的性质及平行线的性质得到结论；

（2）首先利用等腰三角形的性质得∠PAD=∠PDA，设∠PAD=∠PDA=x，利用外角性质易得∠BPC=2x，因为PC⊥BE，得x，得∠ABC的度数；

（3）分类讨论：①当点E在BC的延长线上时，首先利用等腰三角形的性质得CP=CE，易得∠BCP=∠CPE+∠CEP=2∠CEP，由正方形的性质得∠PBA=∠PBC=45°，由全等三角形的判定得△ABP≌△CBP，易得∠BAP=∠BCP=2∠CEP，因为∠BAP+∠PEC=90°，求得∠PEC的度数；②当点E在BC上时，同理得出结论．

试题解析：(1)证明：∵四边形ABCD是菱形，

∴∠PDA=∠PDC,AD=CDAD∥BC，

在△PAD与△PCD中，

，

∴△PAD≌△PCD(SAS)，

∴∠PAD=∠PCD，

又∵AD∥BC，

∴∠AEB=∠PAD=∠PCD；

(2)如图1，

∵PA=PD,

∴∠PAD=∠PDA，

设∠PAD=∠PDA=x，则∠BPC=∠PDC+∠PCD=∠PDA+∠PAD=2x，

∵PC⊥BE，

∴2x+x=90°，

∴x=30°，

∴∠ABC=2x=60°；

(3)①当点E在BC的延长线上时,如图2,

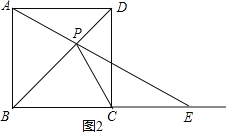
△PCE是等腰三角形,则CP=CE,

∴∠BCP=∠CPE+∠CEP=2∠CEP

∵四边形ABCD是菱形,∠ABC=90°，

∴菱形ABCD是正方形，

∴∠PBA=∠PBC=45°，

在△ABP与△CBP中，

，

∴△ABP≌△CBP(SAS)，

∴∠BAP=∠BCP=2∠CEP，

∵∠BAP+∠PEC=90°,2∠PEC+∠PEC=90°，

∴∠PEC=30°；

②当点E在BC上时，如图3，

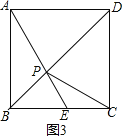
△PCE是等腰三角形，则PE=CE，

∴∠BEP=∠CPE+∠PCE=2∠ECP，

∵四边形ABCD是菱形,∠ABC=90°

∴菱形ABCD是正方形，

∴∠PBA=∠PBC=45°，又AB=BC，BP=BP，

∴△ABP≌△CBP，

∴∠BAP=∠BCP，

∵∠BAP+∠AEB=90°,2∠BCP+∠BCP=90°，

∴∠BCP=30°，

∴∠AEB=60°，

∴∠PEC=180°∠AEB=120°，

综上所述：∠PEC=30°或∠PEC=120°.