题目内容
已知实数a,b满足等式a2-2a-1=0,b2-2b-1=0,则| 1 |
| a |
| 1 |
| b |
分析:此题可以把a,b看作方程x2-2x-1=0的两个根,而
+
=
,然后分类讨论并利用根与系数的关系就可以求出代数式的值.
| 1 |
| a |
| 1 |
| b |
| a+b |
| ab |
解答:解:因为实数a,b满足等式a2-2a-1=0,b2-2b-1=0,
(1)当a=b=1+
或1-
时,原式=
=2
-2或-2
-2;
(2)当a≠b时,可以把a,b看作是方程x2-2x-1=0的两个根.
由根与系数的关系,得a+b=2,ab=-1.
则原式=-2.
故填空答案:-2或2
-2或-2
-2.
(1)当a=b=1+
| 2 |
| 2 |
| a+b |
| ab |
| 2 |
| 2 |
(2)当a≠b时,可以把a,b看作是方程x2-2x-1=0的两个根.
由根与系数的关系,得a+b=2,ab=-1.
则原式=-2.
故填空答案:-2或2
| 2 |
| 2 |
点评:此题要注意分情况考虑,特别不要忘记a=b这种情况,同时也要利用根与系数的关系.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目

 ,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与
,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与 是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.
是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由. ,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与
,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与 是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.
是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.
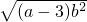 +4=2a,则a+b等于多少?
+4=2a,则a+b等于多少?