��Ŀ����
��֪������y=x2-��2m-1��x+4m-6����1����˵������ÿһ��ʵ��m�������߶�����x���ϵ�һ�����㣻
��2������������x�����������A��x1��0����B��x2��0����x1��x2���ֱ���ԭ������࣬��A��B�����ľ���С��6����m��ȡֵ��Χ��
��3�������ߵĶԳ�����x�ύ�ڵ�C(
| 2m-1 |
| 2 |
 |
| CD |
��������1���������ߵĽ���ʽ��Ϊ����ʽ���������������x��Ľ�������һ���Ƕ�ֵ������m�ı仯���仯��
��2������ɴ��������濼�ǣ���AB�ľ���С��6������Τ�ﶨ�����һ��m��ȡֵ��Χ��
������A��B�ֱ���ԭ�����࣬��˸���Τ�ﶨ����x1x2��0���ݴ˿��������һ��m��ȡֵ��Χ���ۺ�����������ɵó������m��ȡֵ��Χ��
��3������Ҫ�Ȼ���ͼ�Σ��������߶Գ�����y�������Ҳ��������������⣮����˼·һ�£�����ԲM��y����е�ΪD����M��x��Ĵ����费��ΪE������ͨ����ֱ��������ACD��MEB����MEA���зֱ��ʾ��OD��ME�ij�������OD=ME���е�����ϵ���t��ֵ��
��2������ɴ��������濼�ǣ���AB�ľ���С��6������Τ�ﶨ�����һ��m��ȡֵ��Χ��
������A��B�ֱ���ԭ�����࣬��˸���Τ�ﶨ����x1x2��0���ݴ˿��������һ��m��ȡֵ��Χ���ۺ�����������ɵó������m��ȡֵ��Χ��
��3������Ҫ�Ȼ���ͼ�Σ��������߶Գ�����y�������Ҳ��������������⣮����˼·һ�£�����ԲM��y����е�ΪD����M��x��Ĵ����费��ΪE������ͨ����ֱ��������ACD��MEB����MEA���зֱ��ʾ��OD��ME�ij�������OD=ME���е�����ϵ���t��ֵ��
����⣺��1���������֪��y=��x-2����x-2m+3����
�����������x�����������������
��2��0����2m-3��0����
�������mȡ��ֵ������������x�ύ�ڣ�2��0���㣻
��2����y=0����x2-��2m-1��x+4m-6=0����
x1+x2=2m-1��x1x2=4m-6��
��AB��6
��x2-x1��6��
����x2-x1��2��36����x1+x2��2-4x1x2��36��
����2m-1��2-4��4m-6����36��
���-
��x��
����
����A��B�ֱ���ԭ�������֪��x1x2��0��
��4m-6��0��m��
����
�ۺϢ٢ڿɵ�-
��m��
��
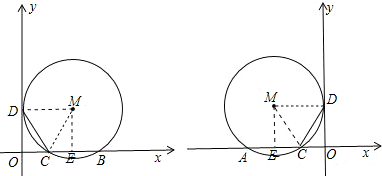
��3���������������m����ԲM��y����е�ΪD����M��x��Ĵ����费��ΪE��
�ٵ�C����x������ʱ��x=
��0��
���
��m��
��
��BC=��CD��
���BC=CD��
OC=
��CD=BC=OB-OC=2-
=
��EC=
BC=
��
OE=MD=OC+CE=
+
=
��
��֪��OD=ME����OD2=ME2
��CD2-OC2=CM2-CE2��
��
��2-��
��2=��
��2-��
��2��
���m=
������m��ȡֵ��Χ��
�ڵ�C����x������ʱ��x=
��0��
���-
��m��
��
ͬ�ٿ����OC=
��CD=AC=
��CE=
��MD=OE=
��
ͬ���У�CD2-OC2=MC2-CE2
��
��2-��
��2=��
��2-��
��2
����ã�m2=
��
��m=��
����������m��ȡֵ��Χ��
������������������
�������������ڷ���������m����m=
��
�����������x�����������������
��2��0����2m-3��0����
�������mȡ��ֵ������������x�ύ�ڣ�2��0���㣻
��2����y=0����x2-��2m-1��x+4m-6=0����
x1+x2=2m-1��x1x2=4m-6��
��AB��6
��x2-x1��6��
����x2-x1��2��36����x1+x2��2-4x1x2��36��
����2m-1��2-4��4m-6����36��
���-
| 1 |
| 2 |
| 11 |
| 2 |
����A��B�ֱ���ԭ�������֪��x1x2��0��
��4m-6��0��m��
| 3 |
| 2 |
�ۺϢ٢ڿɵ�-
| 1 |
| 2 |
| 3 |
| 2 |
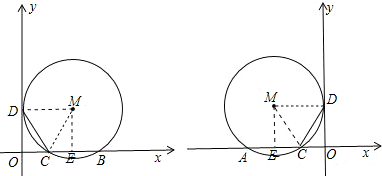
��3���������������m����ԲM��y����е�ΪD����M��x��Ĵ����费��ΪE��
�ٵ�C����x������ʱ��x=
| 2m-1 |
| 2 |
���
| 1 |
| 2 |
| 3 |
| 2 |
��BC=��CD��
���BC=CD��
OC=
| 2m-1 |
| 2 |
| 2m-1 |
| 2 |
| 5-2m |
| 2 |
| 1 |
| 2 |
| 5-2m |
| 4 |
OE=MD=OC+CE=
| 2m-1 |
| 2 |
| 5-2m |
| 2 |
| 2m+3 |
| 4 |
��֪��OD=ME����OD2=ME2
��CD2-OC2=CM2-CE2��
��
| 2m-5 |
| 2 |
| 2m-1 |
| 2 |
| 2m+3 |
| 4 |
| 5-2m |
| 4 |
���m=
| 7 |
| 6 |
�ڵ�C����x������ʱ��x=
| 2m-1 |
| 2 |
���-
| 1 |
| 2 |
| 1 |
| 2 |
ͬ�ٿ����OC=
| 1-2m |
| 2 |
| 5-2m |
| 2 |
| 5-2m |
| 4 |
| 7-6m |
| 4 |
ͬ���У�CD2-OC2=MC2-CE2
��
| 5-2m |
| 2 |
| 1-2m |
| 2 |
| 7-6m |
| 4 |
| 5-2m |
| 4 |
����ã�m2=
| 9 |
| 4 |
��m=��
| 3 |
| 2 |
������������������
�������������ڷ���������m����m=
| 7 |
| 6 |
������������Բ��һԪ���η��̵����֪ʶ�����˶��κ������ۺ�Ӧ�ã��ѶȽϴ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
��֪������y=x2-8x+c�Ķ�����x���ϣ���c���ڣ�������
| A��4 | B��8 | C��-4 | D��16 |
 ��1����b+c��ֵ��
��1����b+c��ֵ�� ��2012•�����һģ����ͼ����ƽ��ֱ������ϵxOy�У���֪������y=x2+bx+c����A��0��3����B��1��0�����㣬����ΪM��
��2012•�����һģ����ͼ����ƽ��ֱ������ϵxOy�У���֪������y=x2+bx+c����A��0��3����B��1��0�����㣬����ΪM��