题目内容
(2004•济宁)已知抛物线y=x2-(2m-1)x+4m-6.(1)试说明对于每一个实数m,抛物线都经过x轴上的一个定点;
(2)设抛物线与x轴的两个交点A(x1,0)和B(x2,0)(x1<x2)分别在原点的两侧,且A、B两点间的距离小于6,求m的取值范围;
(3)抛物线的对称轴与x轴交于点C
 ,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与
,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与 是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.
是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.
【答案】分析:(1)将抛物线的解析式化为交点式,可求得抛物线与x轴的交点其中一个是定值,不随m的变化而变化;
(2)本题可从两个方面考虑:①AB的距离小于6,可用韦达定理求出一个m的取值范围,
②由于A、B分别在原点两侧,因此根据韦达定理有x1x2<0,据此可求出另外一个m的取值范围.综合两种情况即可得出所求的m的取值范围;
(3)本题要先画出图形,分抛物线对称轴在y轴左侧和右侧两种情况进行求解.解题思路一致.假设圆M与y轴的切点为D,过M作x轴的垂线设垂足为E,都是通过在直角三角形ACD和MEB(或MEA)中分别表示出OD和ME的长,根据OD=ME来列等量关系求出t的值.
解答:解:(1)由题意可知:y=(x-2)(x-2m+3),
因此抛物线与x轴的两个交点坐标为:
(2,0)(2m-3,0),
因此无论m取何值,抛物线总与x轴交于(2,0)点;
(2)令y=0,有:x2-(2m-1)x+4m-6=0,则:
x1+x2=2m-1,x1x2=4m-6;
∵AB<6
∴x2-x1<6,
即(x2-x1)2<36,(x1+x2)2-4x1x2<36,
即(2m-1)2-4(4m-6)<36,
解得- <x<
<x< .①
.①
根据A、B分别在原点两侧可知:x1x2<0,
即4m-6<0,m< .②
.②
综合①②可得- <m<
<m< ;
;
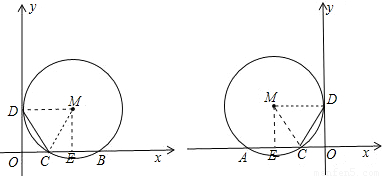
(3)假设存在这样的m,设圆M与y轴的切点为D,过M作x轴的垂线设垂足为E.
①当C点在x正半轴时,x=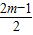 >0,
>0,
因此 <m<
<m< ,
,
∵弧BC=弧CD,
因此BC=CD.
OC=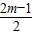 ,CD=BC=OB-OC=2-
,CD=BC=OB-OC=2- =
=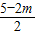 ,EC=
,EC= BC=
BC=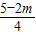 ,
,
OE=MD=OC+CE=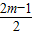 +
+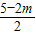 =
=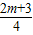 .
.
易知:OD=ME,即OD2=ME2
∴CD2-OC2=CM2-CE2,
(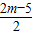 )2-(
)2-(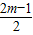 )2=(
)2=(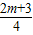 )2-(
)2-(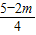 )2;
)2;
解得m= ,符合m的取值范围.
,符合m的取值范围.
②当C点在x负半轴时,x=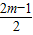 <0,
<0,
因此- <m<
<m< ,
,
同①可求得OC=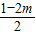 ,CD=AC=
,CD=AC=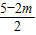 ,CE=
,CE=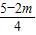 ,MD=OE=
,MD=OE=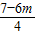 .
.
同理有:CD2-OC2=MC2-CE2
( )2-(
)2-(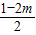 )2=(
)2=( )2-(
)2-(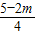 )2
)2
化简得:m2= ,
,
∴m=± ,均不符合m的取值范围,
,均不符合m的取值范围,
因此这种情况不成立.
综上所述,存在符合条件的m,且m= .
.
点评:本题结合圆和一元二次方程的相关知识考查了二次函数的综合应用,难度较大.
(2)本题可从两个方面考虑:①AB的距离小于6,可用韦达定理求出一个m的取值范围,
②由于A、B分别在原点两侧,因此根据韦达定理有x1x2<0,据此可求出另外一个m的取值范围.综合两种情况即可得出所求的m的取值范围;
(3)本题要先画出图形,分抛物线对称轴在y轴左侧和右侧两种情况进行求解.解题思路一致.假设圆M与y轴的切点为D,过M作x轴的垂线设垂足为E,都是通过在直角三角形ACD和MEB(或MEA)中分别表示出OD和ME的长,根据OD=ME来列等量关系求出t的值.
解答:解:(1)由题意可知:y=(x-2)(x-2m+3),
因此抛物线与x轴的两个交点坐标为:
(2,0)(2m-3,0),
因此无论m取何值,抛物线总与x轴交于(2,0)点;
(2)令y=0,有:x2-(2m-1)x+4m-6=0,则:
x1+x2=2m-1,x1x2=4m-6;
∵AB<6
∴x2-x1<6,
即(x2-x1)2<36,(x1+x2)2-4x1x2<36,
即(2m-1)2-4(4m-6)<36,
解得-
 <x<
<x< .①
.①根据A、B分别在原点两侧可知:x1x2<0,
即4m-6<0,m<
 .②
.②综合①②可得-
 <m<
<m< ;
;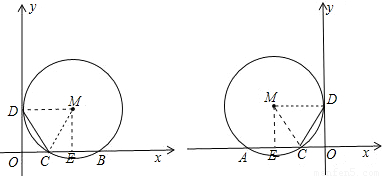
(3)假设存在这样的m,设圆M与y轴的切点为D,过M作x轴的垂线设垂足为E.
①当C点在x正半轴时,x=
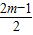 >0,
>0,因此
 <m<
<m< ,
,∵弧BC=弧CD,
因此BC=CD.
OC=
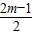 ,CD=BC=OB-OC=2-
,CD=BC=OB-OC=2- =
=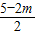 ,EC=
,EC= BC=
BC=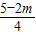 ,
,OE=MD=OC+CE=
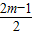 +
+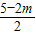 =
=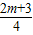 .
.易知:OD=ME,即OD2=ME2
∴CD2-OC2=CM2-CE2,
(
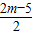 )2-(
)2-(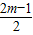 )2=(
)2=(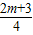 )2-(
)2-(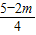 )2;
)2;解得m=
 ,符合m的取值范围.
,符合m的取值范围.②当C点在x负半轴时,x=
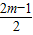 <0,
<0,因此-
 <m<
<m< ,
,同①可求得OC=
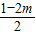 ,CD=AC=
,CD=AC=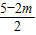 ,CE=
,CE=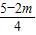 ,MD=OE=
,MD=OE=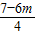 .
.同理有:CD2-OC2=MC2-CE2
(
 )2-(
)2-(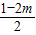 )2=(
)2=( )2-(
)2-(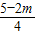 )2
)2化简得:m2=
 ,
,∴m=±
 ,均不符合m的取值范围,
,均不符合m的取值范围,因此这种情况不成立.
综上所述,存在符合条件的m,且m=
 .
.点评:本题结合圆和一元二次方程的相关知识考查了二次函数的综合应用,难度较大.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
(2004•济宁)阅读下面材料:
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式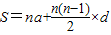 来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=
来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=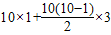 =145.
=145.
用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
假设所有苗木的成活率都是100%,问到哪一年年底,这个镇的苗木面积达到5万亩?
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式
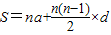 来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=
来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=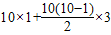 =145.
=145.用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
| 年份 | 2001年 | 2002年 | 2003年 |
| 每年种植苗木的面积(亩) | 4000 | 5000 | 6000 |
| 每年卖出成苗木的面积(亩) | 2000 | 2500 | 3000 |
(2004•济宁)阅读下面材料:
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式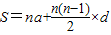 来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=
来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=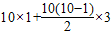 =145.
=145.
用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
假设所有苗木的成活率都是100%,问到哪一年年底,这个镇的苗木面积达到5万亩?
在计算1+4+7+10+13+16+19+22+25+28时,我们发现,从第一个数开始,以后的每个数与它的前一个数的差都是一个相同的定值,具有这种规律的一列数,求和时,除了直接相加外,我们还可以用公式
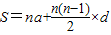 来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=
来计算(公式中的S表示它们的和,n表示数的个数,a表示第一个数的值,d表示这个相差的定值).那么S=1+4+7+10+13+16+19+22+25+28=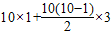 =145.
=145.用上面的知识解决下列问题:
我市某乡镇具有“中国北方乔木之乡”的美称,到2000年底这个镇已有苗木2万亩,为增加农民收入,这个镇实施“苗木兴镇”战略,逐年有计划地扩种苗木.从2001年起,以后每年又比上一年多种植相同面积的苗木;从2001年起每年卖出成苗木,以后每年又比上一年多卖出相同面积的苗木.下表为2001年、2002年、2003年三年种植苗木与卖出成苗木的面积统计数据.
| 年份 | 2001年 | 2002年 | 2003年 |
| 每年种植苗木的面积(亩) | 4000 | 5000 | 6000 |
| 每年卖出成苗木的面积(亩) | 2000 | 2500 | 3000 |
 ,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与
,在(2)的条件下,试判断是否存在m的值,使经过点C及抛物线与x轴的一个交点的⊙M与y轴的正半轴相切于点D,且被x轴截得的劣弧与 是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.
是等弧?若存在,求出所有满足条件的m的值;若不存在,说明理由.