题目内容
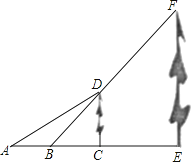
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=![]() ,求CG的长.
,求CG的长.
【答案】
(1)
证明:如图1,连接OD,
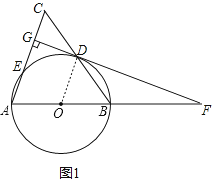
∵AB=AC,
∴∠C=∠ABC,
∵OD=OB,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴∠ODG=∠DGC,
∵DG⊥AC,
∴∠DGC=90°,
∴∠ODG=90°,
∴OD⊥FG,
∵OD是⊙O的半径,
∴直线FG是⊙O的切线.
(2)
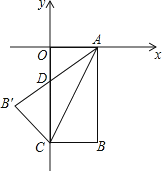
解:如图2,

∵AB=AC=10,AB是⊙O的直径,
∴OA=OD=10÷2=5,
由(1),可得
OD⊥FG,OD∥AC,
∴∠ODF=90°,∠DOF=∠A,
在△ODF和△AGF中,
![]()
∴△ODF∽△AGF,
∴![]() ,
,
∵cosA=![]() ,
,
∴cos∠DOF=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴AF=AO+OF=5![]() ,
,
∴![]() ,
,
解得AG=7,
∴CG=AC﹣AG=10﹣7=3,
即CG的长是3.
【解析】(1)首先判断出OD∥AC,推得∠ODG=∠DGC,然后根据DG⊥AC,可得∠DGC=90°,∠ODG=90°,推得OD⊥FG,即可判断出直线FG是⊙O的切线.
(2)首先根据相似三角形判定的方法,判断出△ODF∽△AGF,再根据cosA=![]() ,可得cos∠DOF=
,可得cos∠DOF=![]() ;然后求出OF、AF的值,即可求出AG、CG的值各是多少.
;然后求出OF、AF的值,即可求出AG、CG的值各是多少.
【考点精析】认真审题,首先需要了解切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.

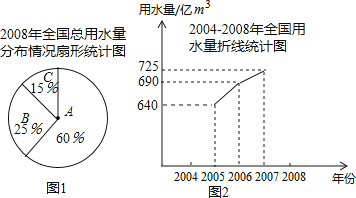
【题目】某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 | 测试成绩(分) | 人数 |
优秀 | 45≤x≤50 | 140 |
良好 | 37.5≤x<45 | 36 |
及格 | 30≤x<37.5 | |
不及格 | x<30 | 6 |

根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有人,达到优秀的人数占本次测试总人数的百分比为%.
(2)本次测试的学生数为人,其中,体质健康成绩为及格的有人,不及格的人数占本次测试总人数的百分比为%.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.