题目内容
阅读材料:求1+2+22+23+24+…+22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22013+22014
将下式减去上式得2S﹣S=22014﹣1
即S=22014﹣1
即1+2+22+23+24+…+22013=22014﹣1
请你仿照此法计算:
(1)1+2+22+23+24+…+210
(2)1+3+32+33+34+…+3n(其中n为正整数).
(1)211-1;(2) (3n+1﹣1).
(3n+1﹣1).
解析试题分析:(1)设S=1+2+22+23+24+…+210,两边乘以2后得到关系式,与已知等式相减,变形即可求出所求式子的值;
(2)同理即可得到所求式子的值.
试题解析:(1)设S=1+2+22+23+24+…+210,
将等式两边同时乘以2得2S=2+22+23+24+…+210+211,
将下式减去上式得:2S﹣S=211-1,即S=211-1,
则1+2+22+23+24+…+210=211-1;
(2)设S=1+3+32+33+34+…+3n,
两边乘以3得:3S=3+32+33+34+…+3n+3n+1,
下式减去上式得:3S-S=3n+1-1,
即S= (3n+1-1),则1+3+32+33+34+…+3n=
(3n+1-1),则1+3+32+33+34+…+3n= (3n+1﹣1).
(3n+1﹣1).
考点:同底数幂的乘法.

练习册系列答案
相关题目
请你自编一道有理数混合运算题并写出计算过程,算式要求同时满足以下条件:
(1)必须含有加、减、乘、除、乘方5种运算;
(2)除数必须是分数;
(3)乘方运算中的底数必须是负分数;
(4)计算结果等于2013.
小兰画了一个函数 的图象如图,那么关于x的分式方程
的图象如图,那么关于x的分式方程 的解是( )
的解是( )
| A.x=1 | B.x="2" | C.x="3" | D.x="4" |
 |+
|+ ﹣1(2)化简:
﹣1(2)化简:
 元,她买了多少本?
元,她买了多少本?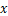 与
与 互为相反数,
互为相反数, 与
与 互为倒数,
互为倒数, ,
,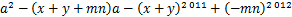 的值.
的值.