题目内容
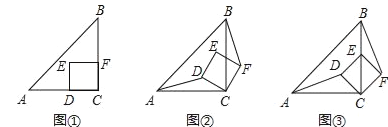
【题目】(1)如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为10的长方形,求正方形纸片A、B的边长.
(2)如图2,将一张正方形纸片D放在一正方形纸片C的内部,阴影部分的面积为4;如图3,将正方形纸片C、D各一张并列放置后构造一个新的正方形,阴影部分的面积为48,求正方形C、D的面积之和.

【答案】(1)A、B的边长分别为4和6;(2)52.
【解析】
(1)设正方形A、B的边长分别为a、b,由题意得:正方形a的边长+正方形B的边长=10,2个正方形A的边长=3个正方形B的边长,根据等量关系列出方程组,再解即可;
(2)设正方形C、D的边长为c、d,由图2得:(c-d)2=4,由图3得:(c+d)2-c2-d2=48,然后两个方程组合可得c2+d2的值.
(1)设正方形A、B的边长分别为a、b,由题意得:![]() ,
,
解得:![]() ,
,
答:正方形A、B的边长分别为6,4;
(2)设正方形C、D的边长为c、d,则:
由图2得:(c-d)2=4,即:c2-2cd+d2=4,
由图3得:(c+d)2-c2-d2=48,即2dc=48,
∴c2+d2-48=4,
∴c2+d2=52,
即正方形C、D的面积和为52.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】根据下表回答问题:
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
(1)272.25的平方根是
(2)![]() = ,
= , ![]() = ,
= , ![]() =
=
(3)设![]() 的整数部分为a,求﹣4a的立方根.
的整数部分为a,求﹣4a的立方根.