题目内容
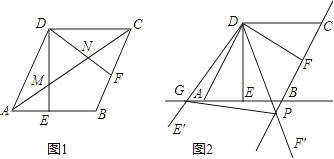
【题目】如图,在矩形ABCD中,AB=![]() ,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为 .
,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为 .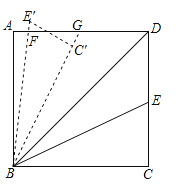
【答案】![]()
【解析】解:过E作EO⊥BD于O,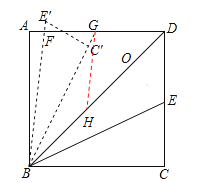
在Rt△ABD中,由勾股定理,得
BD=![]() =
=![]() =14,
=14,
在Rt△ABF中,由勾股定理,得:
BF2=(4![]() )2+(10﹣BF)2 ,
)2+(10﹣BF)2 ,
解得BF=![]() ,
,
AF=10﹣![]() =
=![]() .
.
过G作GH∥BF,交BD于H,
∴∠FBD=∠GHD,∠BGH=∠FBG,
∵FB=FD,
∴∠FBD=∠FDB,
∴∠FDB=∠GHD,
∴GH=GD,
∵∠FBG=∠EBC=![]() ∠DBC=
∠DBC=![]() ∠ADB=
∠ADB=![]() ∠FBD,
∠FBD,
又∵∠FBG=∠BGH,∠FBG=∠GBJ,
∴BH=GH,
设DG=GH=BH=x,则FG=FD﹣GD=![]() ﹣x,HD=14﹣x,
﹣x,HD=14﹣x,
∵GH∥FB,
∴![]() ,即
,即![]() ,
,
解得x=![]() .
.
所以答案是:![]() .
.
【考点精析】通过灵活运用旋转的性质,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目