题目内容
9、在直角坐标系中，我们把横、纵坐标都为整数的点叫做整点．且规定，正方形的内部不包含边界上的点．观察如图所示的中心在原点、一边平行于x轴的正方形：边长为1的正方形内部有1个整点，边长为3的正方形内部有9个整点，…，则边长为8的正方形内部整点个数为（ ）分析：求出边长为1、2、3、4、5、6、7、的正方形的整点的个数，得到边长为1和2的正方形内部有1个整点，边长为3和4的正方形内部有9个整点，边长为5和6的正方形内部有25个整点，推出边长为7和8的正方形内部有49个整点，即可得出答案．
解答：解法1：边长为1的正方形内部有1个整点：1，
边长为2的正方形内部有1个整点：1，
边长为3的正方形内部有9个整点：1+4×2，
边长为4的正方形内部有9个整点：1+4×2，
边长为5的正方形内部有25个整点：1+4×6，
边长为6的正方形内部有25个整点：1+4×6，
边长为7的正方形内部有49个整点：1+4×12，
则边长为8的正方形内部整点个数为：1+4×12=49（个）．
解法2：设边长为8的正方形内部的整点的坐标为（x，y），x，y都为整数．
则-4＜x＜4，-4＜y＜4，
故x只可取-3，-2，-1，0，1，2，3共7个，y只可取-3，-2，-1，0，1，2，3共7个，
它们共可组成点（x，y）的数目为7×7=49（个）
故选B．
边长为2的正方形内部有1个整点：1，
边长为3的正方形内部有9个整点：1+4×2，
边长为4的正方形内部有9个整点：1+4×2，
边长为5的正方形内部有25个整点：1+4×6，
边长为6的正方形内部有25个整点：1+4×6，
边长为7的正方形内部有49个整点：1+4×12，
则边长为8的正方形内部整点个数为：1+4×12=49（个）．
解法2：设边长为8的正方形内部的整点的坐标为（x，y），x，y都为整数．
则-4＜x＜4，-4＜y＜4，
故x只可取-3，-2，-1，0，1，2，3共7个，y只可取-3，-2，-1，0，1，2，3共7个，
它们共可组成点（x，y）的数目为7×7=49（个）
故选B．
点评：本题主要考查对正方形的性质，坐标与图形的性质等知识点的理解和掌握，根据已知总结出规律是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
（2005•遵义）在直角坐标系中，我们把横、纵坐标都为整数的点叫做整点．设坐标轴的单位长度为1厘米，整点P从原点O出发，速度为1厘米/秒，且整点P作向上或向右运动（如图所示）．运动时间（秒）与整点（个）的关系如下表：
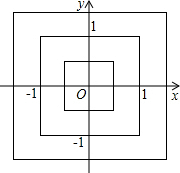在直角坐标系中，我们把横、纵坐标都是整数的点叫做整点，且规定：正方形内部不包含边界上的点．观察如图所示的中心在原点、一边平行于x轴的正方形：边长为1的正方形内部有1个整点，边长为2的正方形内部有1个整点，边长为3的正方形内部有9个整点，…，则边长为9的正方形内的整点个数为（ ）| A、64 | B、49 | C、36 | D、81 |
在直角坐标系中，我们把横、纵坐标都为整数的点叫作整点.设坐标轴的单位长度为1cm，整点P从原点O出发，速度为1cm/s，且整点P作向上或向右运动，运动时间（s）与整点（个）的关系如下表：
|
整点P从原点O出发 的时间（s） |
可以得到整点P的坐标 |
可以得到整点 P的个数 |
|
1 |
（0，1），（1，0） |
2 |
|
2 |
（0，2），（1，1），（2，0） |
3[来源:] |
|
3 |
（0，3）（1，2）（2，1）（3，0） |
4 |
|
… |
… |
… |
根据上表中的规律，回答下列问题：
⑴当整点P从点O出发4s时可得到的整点P有 个；
⑵当整点P从点O出发8s时，在直角坐标系中描出可以得到的整点，并顺次连接这些整点；
⑶当整点P从点O出发 s时，可以到达整点（16，4）的位置；
⑷当整点P（x,y）从点O出发30s时，当整点P（x,y）恰好在直线y＝2x－6上，求整点P的坐标.
