题目内容
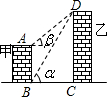如图，线段AB、DC分别表示甲、乙两建筑物的高．AB⊥BC，DC⊥BC，从B点测得点D的仰角为α，从A点测得点D的仰角为β．已知甲乙两建筑物之间的距离为a，甲建筑物的高AB为分析：首先分析图形，根据题意构造直角三角形．本题涉及到两个直角三角形△ADE、△DBC，应借助AE=BC，求出DC，DE，从而求出AB即可．
解答：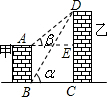
解：过点A作AE⊥CD于点E．
根据题意，得∠DBC=∠α，∠DAE=∠β，AE=BC=a，
在Rt△AED中，tan∠DAE=tanβ=
，
∴DE=AEtanβ=atanβ，
在Rt△DCB中，tan∠DBC=tanα=
，
∴DC=BCtanα=atanα，
∴AB=EC=atanα-atanβ=a（tanα-tanβ）．
故答案为：a（tanα-tanβ）．
解：过点A作AE⊥CD于点E．根据题意，得∠DBC=∠α，∠DAE=∠β，AE=BC=a，
在Rt△AED中，tan∠DAE=tanβ=
| DE |
| AE |
∴DE=AEtanβ=atanβ，
在Rt△DCB中，tan∠DBC=tanα=
| DC |
| BC |
∴DC=BCtanα=atanα，
∴AB=EC=atanα-atanβ=a（tanα-tanβ）．
故答案为：a（tanα-tanβ）．
点评：此题主要考查了解直角三角形的应用，借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形是解题关键．
练习册系列答案
相关题目
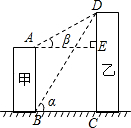从A点测得D点的仰角β为30°，已知甲建筑物高AB=36米．
14、如图，线段AB、DC分别表示甲、乙两座楼房的高，AB⊥BC，DC⊥BC，两建筑物间距离BC=30米，若甲建筑物高AB=28米，在点A测得D点的仰角α=45°，则乙建筑物高DC=
（2013•呼伦贝尔）如图，线段AB、DC分别表示甲乙两座建筑物的高，AB⊥BC，DC⊥BC，两建筑物的水平距离BC为30米，若甲建筑物的高AB=28米，在点A处观察乙建筑物顶部D的仰角为60°，求乙建筑物的高度 （结果保留1位小数，
（2012•呼和浩特）如图，线段AB，DC分别表示甲、乙两建筑物的高．某初三课外兴趣活动小组为了测量两建筑物的高，用自制测角仪在B处测得D点的仰角为α，在A处测得D点的仰角为β．已知甲、乙两建筑物之间的距离BC为m．请你通过计算用含α、β、m的式子分别表示出甲、乙两建筑物的高度．