题目内容
（2012•呼和浩特）如图，线段AB，DC分别表示甲、乙两建筑物的高．某初三课外兴趣活动小组为了测量两建筑物的高，用自制测角仪在B处测得D点的仰角为α，在A处测得D点的仰角为β．已知甲、乙两建筑物之间的距离BC为m．请你通过计算用含α、β、m的式子分别表示出甲、乙两建筑物的高度．分析：首先分析图形，根据题意构造直角三角形．本题涉及到两个直角三角形△ADM、△DBC，应借助AE=BC，求出DC，DM，从而求出AB即可．
解答：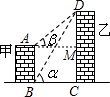
解：过点A作AM⊥CD，垂足为M，
在Rt△BCD中，tanα=
，
∴CD=BC•tanα=mtanα，
在Rt△AMD中，tanβ=
，
∴DM=AM•tanβ=mtanβ，
∴AB=CD-DM=m（tanα-tanβ）．
故甲建筑物的高度为m（tanα-tanβ），乙建筑物的高度为mtanα．
解：过点A作AM⊥CD，垂足为M，在Rt△BCD中，tanα=
| CD |
| BC |
∴CD=BC•tanα=mtanα，
在Rt△AMD中，tanβ=
| DM |
| AM |
∴DM=AM•tanβ=mtanβ，
∴AB=CD-DM=m（tanα-tanβ）．
故甲建筑物的高度为m（tanα-tanβ），乙建筑物的高度为mtanα．
点评：此题主要考查了解直角三角形的应用，借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
（2012•呼和浩特）如图，在一长方形内有对角线长分别为2和3的菱形，边长为1的正六边形和半径为1的圆，则一点随机落在这三个图形内的概率较大的是（ ）
（2012•呼和浩特）实数a，b在数轴上的位置如图所示，则
（2012•呼和浩特）如图，一次函数y=kx+b与反比例函数