题目内容
完成下列各题：
（1）三根垂直地面的木杆甲、乙、丙，在路灯下乙．丙的影子如图1所示．试确定路灯灯泡的位置，再作出甲的影子．（不写作法，保留作图痕迹）
（2）如图2，在平行四边形ABCD中，点E，F分别在AB，CD上，AE=CF．求证：DE=BF．
（1）三根垂直地面的木杆甲、乙、丙，在路灯下乙．丙的影子如图1所示．试确定路灯灯泡的位置，再作出甲的影子．（不写作法，保留作图痕迹）
（2）如图2，在平行四边形ABCD中，点E，F分别在AB，CD上，AE=CF．求证：DE=BF．
分析：（1）首先利用乙、丙的影子得出光源的位置，进而得出甲的影子；
（2）利用平行四边形的性质得出CD=AB，CD∥AB，进而得出四边形DEBF是平行四边形即可得出答案．
（2）利用平行四边形的性质得出CD=AB，CD∥AB，进而得出四边形DEBF是平行四边形即可得出答案．
解答：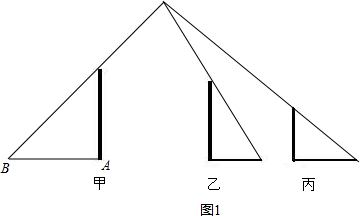
（1）解：如图所示：AB即为甲的影子；
（2）证明：∵在平行四边形ABCD中，
∴CD=AB，CD∥AB，
∵AE=CF，
∴DF=BE，
又∵CD∥AB，
∴四边形DEBF是平行四边形，
∴DE=BF．
（1）解：如图所示：AB即为甲的影子；（2）证明：∵在平行四边形ABCD中，
∴CD=AB，CD∥AB，
∵AE=CF，
∴DF=BE，
又∵CD∥AB，
∴四边形DEBF是平行四边形，
∴DE=BF．
点评：此题主要考查了中心投影的性质和平行四边形的判定与性质，得出光源的位置是解题关键．
练习册系列答案
相关题目
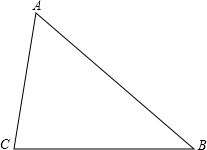如图，在△ABC中，∠B=40°，∠C=80°，按要求完成下列各题：
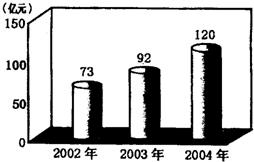下图显示的是今年2月25日《太原日报》刊登的太原市2002年至2004年财政总收入完成情况，图中数据精确到1亿元，根据图中数据完成下列各题：
（2012•泰宁县质检）如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：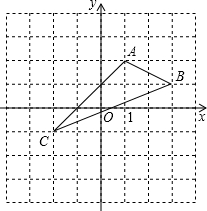
如图，在平面直角坐标系中完成下列各题：