题目内容
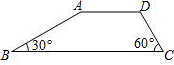如图，已知梯形ABCD中，AD∥BC，∠B=30°，∠C=60°，AD=4，AB=3| 3 |
| A、8 | ||
B、（4+3
| ||
| C、10 | ||
D、6
|
分析：过D作AB的平行线DE构造一个平行四边形及直角三角形，则BE=AD，利用60°的正弦值可得CE的值，加上BE的值即为BC的长．
解答：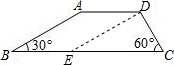
解：作DE∥AB交BC于点E，
∵AD∥BC，
∴四边形ABED是平行四边形，
∴BE=AD=4，ED=AB=3
，∠DEC=30°，
∵∠C=60°，
∴∠EDC=90°，
∵sin60°=
，
∴EC=3
÷sin60°=6，
BC=EC+BE=10，
故选C．
解：作DE∥AB交BC于点E，∵AD∥BC，
∴四边形ABED是平行四边形，
∴BE=AD=4，ED=AB=3
| 3 |
∵∠C=60°，
∴∠EDC=90°，
∵sin60°=
| DE |
| EC |
∴EC=3
| 3 |
BC=EC+BE=10，
故选C．
点评：考查利用解直角三角形求相应边长；作梯形一腰的平行线构造平行四边形和直角三角形是解决本题的难点．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
9、如图，已知梯形ABCD中，AD∥BC，BE平分∠ABC，BE⊥CD，∠A=110°，AD=3，AB=5，则BC的长为（ ）
点到达终点时，另一点也随之停止．过Q作QD∥AB交AC于点D，连接PD，设运动时间为t秒时，四边形BQDP的面积为s．
（2007•遂宁）如图，已知等腰△ABC的面积为4cm2，点D、E分别是AB、AC边的中点，则梯形DBCE的面积为