Question

【题目】如图，直线与x轴交于点B，与轴交于点，已知二次函数的图象经过点B、和点。

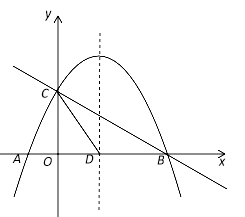
（1）求该二次函数的关系式；

（2）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标。

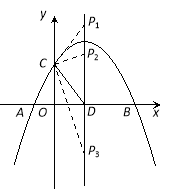
（3）若抛物线的对称轴与x轴的交点为点D，则在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由。

Answer 1

【答案】（1）、；（2）、时，最大面积为．E（2，1）；（3）、P1 （，4） P2 （，） P3（，）.

【解析】

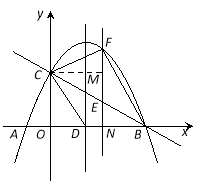
试题分析：（1）、首先根据一次函数得出点B和点C的坐标，然后利用待定系数法求出函数解析式；（2）、过点C作CM⊥EF垂足为M，设E（a，），则F（a，），然后根据四边形的面积等于三个三角形的面积之和得出函数解析式，从而得出最大值；（3）、根据等腰三角形的性质得出点P的坐标.

试题解析：（1）、对于直线，当时，当时

∴B（4，0），C（0，2）。

∵二次函数的图象过点，

∴可设二次函数的关系式为

又∵该函数图象过点、

∴

解之，得，

∴抛物线的表达式。

（2）、过点C作CM⊥EF垂足为M,

设E（a，），则F（a，）

∴ EF==．（0≤a≤4）

∴

=+=+=．（0≤a≤4）

当时，的最大值为．此时E（2，1）。

（3）、在抛物线的对称轴上存在点P，使△PCD是以CD为腰的等腰三角形。

∴ P1 （，4） P2 （，） P3（，）