Question

【题目】综合与探究

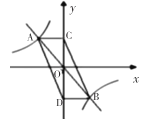
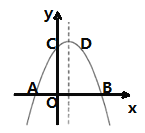
如图，已知抛物线与轴交于、两点，与轴交于点，顶点坐标为点．

（1）求此抛物线的解析式；

（2）点为抛物线对称轴上一点，当最小时，求点坐标；

（3）在第一象限的抛物线上有一点，当面积最大时，求点坐标；

（4）在轴下方抛物线上有一点，面积为6，请直接写出点的坐标．

Answer 1

【答案】（1）；（2）点坐标为；（3）点坐标为；（4）、．

【解析】

(1)设抛物线解析式为，将点B的坐标代入，即可求解；
(2)点A关于函数对称轴的对称点为B，连接BC交函数对称轴于点P，此时点P即为所求点，即可求解；
(3)利用，结合二次函数的最值问题，即可求解；

(4)利用三角形面积公式可求得点H的纵坐标，即可求解．

(1) ∵抛物线的顶点坐标为点()

设抛物线解析式为，

将点代入得：，

解得：，

∴解析式为：；

(2) 函数的表达式为：，

令，则，

解得：或，

令，则，
故点A、C的坐标分别为(-1，0)、(0，2)，
点A关于函数对称轴的对称点为B，连接BC交函数对称轴于点P，此时点P即为所求点，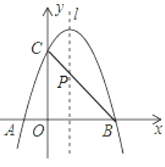

设直线BC的表达式为：，

将点B、C的坐标代入一次函数表达式：得：

，

解得：，

故直线BC的表达式为：，
当时，，

故点的坐标为；
(3)过点M作MH∥y轴交AB于点H，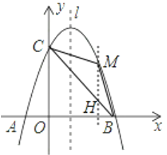

设点，则点，

∴当时，最大，

将代入得：，

此时，点M的坐标为：；

(4)设点H的纵坐标为y，

，

解得：，

∵点在轴下方，

∴，

将代入得：，

解得：，

∴点的坐标为：，